
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ответ:, , ,
Пример 1.1.3. Автомобиль движется по выпуклому мосту. Траектория движения автомобиля изменяется по закону 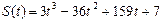 , м; время t - в секундах. Определить скорость и ускорение центра масс автомобиля в тот момент времени, когда он находится на вершине моста, а радиус кривизны траектории
, м; время t - в секундах. Определить скорость и ускорение центра масс автомобиля в тот момент времени, когда он находится на вершине моста, а радиус кривизны траектории  .
.

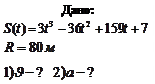 Решение:
Решение:
 Мгновенная скорость
Мгновенная скорость  . По определению ускорения
. По определению ускорения 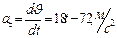 ,
, 
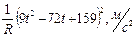 , где
, где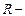 радиус кривизны траектории в данный момент времени. Определим момент времени
радиус кривизны траектории в данный момент времени. Определим момент времени  , когда автомобиль находится на вершине моста, т.к. в этот момент времени скорость автомобиля достигает минимума и
, когда автомобиль находится на вершине моста, т.к. в этот момент времени скорость автомобиля достигает минимума и 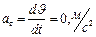 .
. 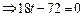 ,
, 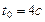 . Т.о. скорость на вершине моста
. Т.о. скорость на вершине моста  . Полное ускорение
. Полное ускорение 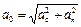
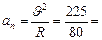
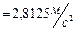 . Направление полного ускорения совпадает с направлением нормального ускорения, т.е. вектор
. Направление полного ускорения совпадает с направлением нормального ускорения, т.е. вектор 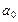 направлен вертикально вниз.
направлен вертикально вниз.
Ответ: 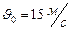 ,
, 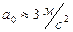 .
.
Пример 1.1.4. Даны уравнения движения точки (время t - в секундах) 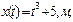

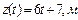 . Найти радиус кривизны траектории в точке, где скорость движения точки
. Найти радиус кривизны траектории в точке, где скорость движения точки 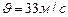 .
.

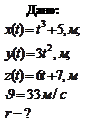 Решение:
Решение:
 Найдем проекции скорости движения точки на оси координат
Найдем проекции скорости движения точки на оси координат 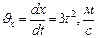 ,
, 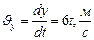 ,
,  . Модуль вектора скорости выражается через проекции:
. Модуль вектора скорости выражается через проекции: 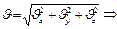
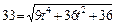 . Возведем в квадрат правую и левую части уравнения и получим
. Возведем в квадрат правую и левую части уравнения и получим 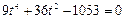 корни уравнения:
корни уравнения: 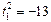 - (не имеет смысла) и
- (не имеет смысла) и 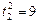 . Получаем время
. Получаем время  .
.
Найдем проекции ускорения на оси координат 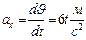 ,
,  ,
, 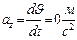 . Модуль вектора полного ускорения:
. Модуль вектора полного ускорения: 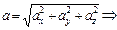
 . По определению
. По определению 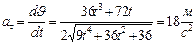 . Полное ускорение
. Полное ускорение 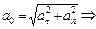 нормальное ускорение
нормальное ускорение 
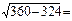
 . Радиус кривизны в данной точке
. Радиус кривизны в данной точке  .
.
Ответ: 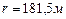 .
.
Пример 1.1.5. Определить скорость, ускорение и зависимость пути от времени, если ускорение тела обратно пропорционально скорости и направлено в сторону, противоположную ей.
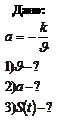
 Решение:
Решение:
 По определению ускорения
По определению ускорения 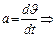
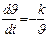 ;
;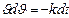 . Проинтегрируем обе части равенства:
. Проинтегрируем обе части равенства: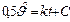 . Выражение для скорости имеет вид:
. Выражение для скорости имеет вид: ; для ускорения
; для ускорения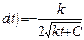 . Постоянная интегрирования
. Постоянная интегрирования 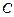 определяется из условия
определяется из условия 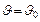 при
при 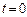 , откуда
, откуда 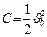 . С учетом
. С учетом 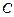 получаем
получаем 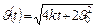 ;
;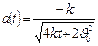 . По определению мгновенной скорости
. По определению мгновенной скорости 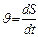 . Находим
. Находим 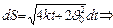

 . Постоянная интегрирования
. Постоянная интегрирования 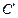 определяется из условия
определяется из условия 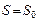 при
при 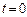 , откуда
, откуда  . Окончательно
. Окончательно  . Ответ:
. Ответ: 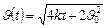 ;
; ;
;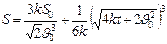 .
.

 Вращение тела вокруг неподвижной оси.
Вращение тела вокруг неподвижной оси.
При вращательном движении абсолютно твердого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат на  одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может быть подвижной и неподвижной (напр., ось вращения колеса движущегося автомобиля относительно машины неподвижна, а относительно дороги перемещается); может располагаться внутри тела или за его пределами.
одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может быть подвижной и неподвижной (напр., ось вращения колеса движущегося автомобиля относительно машины неподвижна, а относительно дороги перемещается); может располагаться внутри тела или за его пределами.
Тело, вращающееся вокруг неподвижной оси, имеет одну степень свободы. Проведем радиус-вектор некоторой точки в момент времени 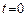 и в любой другой момент времени
и в любой другой момент времени 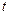 . Угол между этими двумя положениями радиуса-вектора определяет угол поворота
. Угол между этими двумя положениями радиуса-вектора определяет угол поворота 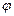 тела. При вращении тела угол
тела. При вращении тела угол 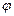 - величина переменная, зависящая от времени t. При вращении твердого тела проекция радиуса-вектора каждой его точки на плоскость, перпендикулярную оси вращения за малый промежуток времени dt поворачивается на один и тот же угол
- величина переменная, зависящая от времени t. При вращении твердого тела проекция радиуса-вектора каждой его точки на плоскость, перпендикулярную оси вращения за малый промежуток времени dt поворачивается на один и тот же угол  . Здесь
. Здесь 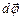 -вектор, длина которого равна углу поворота, а направление определяется в соответствии с правилом правого винта и совпадает с осью вращения – т.о. положение тела в пространстве определяется углом поворота вокруг оси вращения. Но за одинаковые отрезки времени
-вектор, длина которого равна углу поворота, а направление определяется в соответствии с правилом правого винта и совпадает с осью вращения – т.о. положение тела в пространстве определяется углом поворота вокруг оси вращения. Но за одинаковые отрезки времени 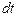 разные точки тела проходят разные расстояния
разные точки тела проходят разные расстояния 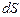 : чем дальше от оси вращения, тем больший путь проходит точка. Т.о. скорости
: чем дальше от оси вращения, тем больший путь проходит точка. Т.о. скорости 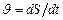 у разных точек тоже разные. Поэтому для описания вращательного движения неудобно пользоваться понятиями «путь», «скорость», «ускорение» точки.
у разных точек тоже разные. Поэтому для описания вращательного движения неудобно пользоваться понятиями «путь», «скорость», «ускорение» точки.
Мерой перемещения служит вектор 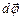 элементарного поворота тела.
элементарного поворота тела.
Опр. 1.1.12. Скорость изменения угла называется угловой скоростью и  является вектором:
является вектором: 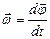 или
или  (1.1.14)
(1.1.14)
Вектор угловой скорости направлен вдоль оси вращения таким образом, чтобы из его конца вращение тела было видно происходящим против часовой стрелки. Направление 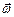 совпадает с направлением поступательного движения буравчика, рукоятка которого вращается вместе с телом.
совпадает с направлением поступательного движения буравчика, рукоятка которого вращается вместе с телом.
Случай 1. Пусть произвольная точка 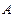 некоторого тела вращается вокруг неподвижной оси, при этом описывая окружность радиуса
некоторого тела вращается вокруг неподвижной оси, при этом описывая окружность радиуса 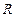 . За малое время
. За малое время 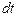 эта точка проходит по дуге окружности путь
эта точка проходит по дуге окружности путь 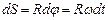 (из 1.1.14). Из данного выражения можно получить два важных вывода:
(из 1.1.14). Из данного выражения можно получить два важных вывода:
1) разделим правую и левую части равенства на 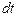 и получим значение модуля скорости
и получим значение модуля скорости  - (1.1.15)
- (1.1.15)
мы получили формулу, связывающую линейную скорость с угловой.
2) т.к.  , то проинтегрировав правую и левую части равенства, получим
, то проинтегрировав правую и левую части равенства, получим 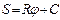 , где постоянная интегрирования
, где постоянная интегрирования 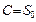 , но при движении по окружности обычно полагают
, но при движении по окружности обычно полагают 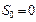 и получаем формулу, связывающую путь и угол поворота:
и получаем формулу, связывающую путь и угол поворота:
 (1.1.16)
(1.1.16)
Средняя угловая скорость определяется как 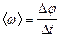 . (1.1.17)
. (1.1.17)
Размерность: 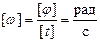 .
.
Опр. 1.1.13. Изменение 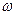 со временем определяется величиной углового ускорения
со временем определяется величиной углового ускорения 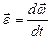 или
или 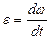 (1.1.18)
(1.1.18)
Вектор углового ускорения 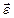 совпадает по направлению с вектором угловой скорости
совпадает по направлению с вектором угловой скорости 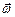 в случае ускоренного вращения
в случае ускоренного вращения  и противоположен ему по направлению в случае замедленного вращения
и противоположен ему по направлению в случае замедленного вращения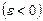 .
.
Случай 2. Пусть т. , рассмотренная в случае 1, вращается ускоренно вокруг неподвижной оси. При движении по кривой полное ускорение
, рассмотренная в случае 1, вращается ускоренно вокруг неподвижной оси. При движении по кривой полное ускорение 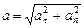 , где
, где
 и
и  . Т.о.
. Т.о. 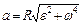 (1.1.19)
(1.1.19)
Среднее угловое ускорение определяется как  . (1.1.20)
. (1.1.20)
Размерность: 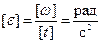 .
.
Опр. 1.1.14. Вращение тела вокруг неподвижной оси называется равномерным, если 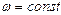 . Тогда по 1.1.14
. Тогда по 1.1.14 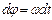 и
и 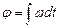
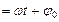 , где
, где 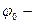 значение постоянной интегрирования при
значение постоянной интегрирования при 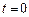 . Т.о.
. Т.о. 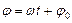 - уравнение равномерного вращения.
- уравнение равномерного вращения.
Опр. 1.1.15. Вращение тела вокруг неподвижной оси называется равнопеременным, если 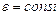 . Тогда угловая скорость
. Тогда угловая скорость  является функцией времени и по 1.1.18 получим
является функцией времени и по 1.1.18 получим 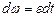 , а после интегрирования -
, а после интегрирования - 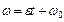 , где
, где 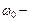 значение постоянной интегрирования при
значение постоянной интегрирования при 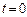 . Применим формулу 1.1.4 и получим
. Применим формулу 1.1.4 и получим 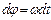 и
и 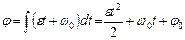 , где
, где значение постоянной интегрирования при
значение постоянной интегрирования при  . Т.о.
. Т.о.  - уравнение равнопеременного вращения.
- уравнение равнопеременного вращения.
Уравнения вращательного и поступательного движения.
| Поступательное движение | Связь между величинами | Вращение тела вокруг неподвижной оси | ||
| Кинетическое уравнение движения (вращения) | 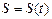 , где , где 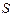 - длина пути, пройденного точкой от начала координат. - длина пути, пройденного точкой от начала координат.
| 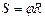 , где R — радиус вращения точки , где R — радиус вращения точки
| 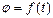 , где , где -угол поворота тела. -угол поворота тела.
| |
| Средняя (средняя угловая) скорость | 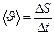
| 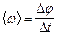
| ||
| Мгновенная (мгновенная угловая) скорость. | 
| 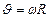 , ,
| 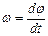
| |
| Среднее (среднее угловое) ускорение | 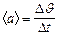
| 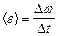
| ||
| Мгновенное (мгновенное угловое) ускорение |
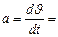 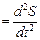
| Полное ускорение 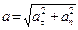
| Модуль ускорения
|
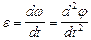
|
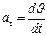
|
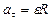 , ,
| |||
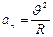
| 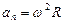 , ,
| |||
| Уравнение равномерного движения (вращения) | 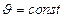 ; ; 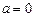 ; ; 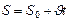
|  ; ;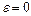 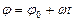
| ||
| Уравнение равнопеременного движения (вращения) | 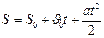
| 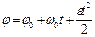
| ||
| Скорость равнопеременного движения (вращения) | 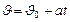 , ,
|  , ,
|
Если вращение является равномерным, т.е. происходит с постоянной угловой скоростью, то такое движение будет периодическим. Для описания периодического движения используют понятия периода и частоты вращательного движения. При этом величину ω иногда называют угловой частотой вращения.
Опр. 1.1.16. Периодом обращения  тела называется время, в течение которого тело поворачивается вокруг неподвижной оси вращения на угол
тела называется время, в течение которого тело поворачивается вокруг неподвижной оси вращения на угол 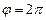 :
: 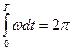 . (1.1.16)
. (1.1.16)
Опр. 1.1.17. Частота вращения - число оборотов в единицу времени  , или
, или 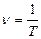 , (1.1.17)
, (1.1.17)
где N  — число оборотов, совершаемых за время t, T — период вращения (время одного оборота).
— число оборотов, совершаемых за время t, T — период вращения (время одного оборота).
Пример 1.1.6. Маховик вращался с постоянной частотой  , потом начал вращаться равноускоренно. Через 8 с вращение маховика опять сделалось равномерным, но уже с частотой
, потом начал вращаться равноускоренно. Через 8 с вращение маховика опять сделалось равномерным, но уже с частотой 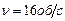 . Определить угловое ускорение
. Определить угловое ускорение 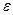 маховика и количество оборотов, сделанных маховиком за время равноускоренного движения.
маховика и количество оборотов, сделанных маховиком за время равноускоренного движения.

 Решение:
Решение:
 Воспользуемся формулой для средней угловой скорости
Воспользуемся формулой для средней угловой скорости 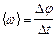 и найдем путь, пройденный маховиком за время равноускоренного движения
и найдем путь, пройденный маховиком за время равноускоренного движения 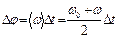 . Учитывая, что
. Учитывая, что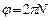 и
и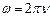 , получаем
, получаем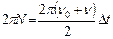 и
и 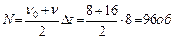 . Учитывая, что
. Учитывая, что
среднее угловое ускорение маховика
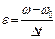
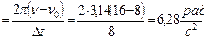 .
.
Ответ: 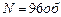 ,
, 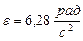 .
.
|
|
Дата добавления: 2014-01-11; Просмотров: 882; Нарушение авторских прав?; Мы поможем в написании вашей работы!