Выборочная дисперсия. Правила расчета дисперсии

До сих пор термин "дисперсия" использовался в смысле теоретической дисперсии, то есть относящейся ко всей генеральной совокупности. Для целей, которые прояснятся при обсуждении регрессионного анализа, целесообразно ввести понятие выборочной дисперсии. Для выборки из п наблюдений х₁,...х _п выборочная дисперсия определяется как среднеквадратичное отклонение в выборке:

Var (x) = 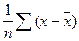² 9.

Сделаем три важных замечания:

1. Определенная таким образом выборочная дисперсия представляет собой смещенную оценку теоретической дисперсии. Выборочная дисперсия, определенная как

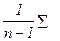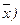s² = (x - ² 10.

является несмещенной оценкой s². Отсюда следует, что ожидаемое значение величины Var (x) равно [(n - 1)/ n ] s² и что, следовательно, она имеет отрицательное смещение. Отметим, что если размер выборки п становится большим, то (п - 1)/ п стремится к единице и, таким образом, математическое ожидание величины Var (x) стремится к s². Можно показать, что ее предел по вероятности (plim) равен s² и, следовательно, она является примером состоятельной оценки, которая смещена для небольших выборок.

2. Так как величина s² является несмещенной, то в некоторых работах ее часто определяют как выборочную дисперсию и либо избегают ссылок на Var(x), либо дают ей какое-то другое название. В русскоязычной литературе величина Var (x) обычно называется выборочной дисперсией, а s² -"исправленной" или несмещенной, выборочной дисперсией. К сожалению, общепринятой договоренности по этому поводу нет.

3. Поскольку указанная договоренность отсутствует, отсутствует и договоренность относительно условного обозначения данного понятия, и для этого используются самые различные символы. Мы условимся теоретическую (или генеральную) дисперсию переменной х обозначать как рор.var (x) или s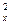. Если ясно, о какой переменной идет речь, то нижний индекс может быть опущен. Выборочную дисперсию будем обозначать как Var (х).

Почему выборочная дисперсия в среднем занижает значение теоретической дисперсии? Причина заключается в том, что она вычисляется как среднеквадратичное отклонение от выборочного среднего, а не от истинного значения. Так как выборочное среднее автоматически находится в центре выборки, то отклонения от него в среднем меньше отклонений от теоретического среднего значения.

Существует несколько простых и очень полезных правил для расчета дисперсии, являющихся аналогами правил для ковариации, рассмотренных в разделе 2.

Правило дисперсии 1.

Если у = v + w, то Var (y) = Var (v) + Var (w) + 2 Cov (v,w) 11.

Правило дисперсии 2.

Если y = a z, где а является постоянной, то Var (y) = a ² Var (z) 12.

Правило дисперсии 3.

Если у = а, где а является постоянной, то Var (y) = 0 13.

Правило дисперсии 4.

Если у = v + a, где a является постоянной, то Var (y) = Var (v). 14.

Кроме того, заметим, что дисперсия переменной х может рассматриваться как ковариация между двумя величинами х:

Var (x) = 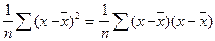= Cov (x, x) 15.

Учитывая это правило, мы можем воспользоваться правилами расчета выборочной ковариации, чтобы вывести правила расчета дисперсии. Кроме того, мы можем получить другую формулу для представления Var (x), используя соотношение (15) для выборочной ковариации.

Var (x) = 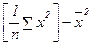16.

Если две переменные независимы и, следовательно, их совокупная ковариация равняется нулю, то теоретическая дисперсия суммы этих переменных будет равна сумме их теоретических дисперсий:

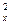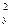
pop.var (x + y) = pop.var (x) + pop. var (y) + 2 pop.cov (x, y) = pop.var (x) + + pop.var (y) = s+ s 17.

Из данного результата можно получить общее правило о том, что теоретическая дисперсия суммы любого числа переменных равняется сумме их дисперсий при условии, что наблюдения независимы друг от друга. При этом можно показать, что если случайная переменная х имеет дисперсию s², то дисперсия выборочного среднего 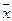будет равна s²/ п, где п - число наблюдений в выборке:

pop.var (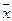) = pop.var 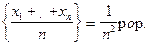var (x₁ +... + xvar (x₁) +...

+ pop.var (x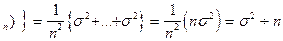 18.

Дата добавления: 2014-01-20