Критерий Михайлова

В критерии Михайлова исследуются частотные свойства характеристического многочлена: р =σ+ jω т.е. р = jω.

D(p) = b₀ * рⁿ + b₁ * р^n-1 + b₂ * p^n-2 + … + b_n-1 * p + b_n

D(p) – характеристический многочлен.

Разложим характеристический многочлен на сомножители:

b₀ * (р – р₁) * (р₁ – р₂)* … (р – р_ί)* … (р – р_n)

На комплексной плоскости исследуем поведение вектора для р_ί корня при изменении р = -j∞ до р = j∞

Оказывается для обеспечения устойчивости системы необходимо и достаточно, чтобы при прохождении точки р = jω мнимой оси в положительном направлении от р = -j∞ до р = j∞ приращение аргумента D(p) было равно nπ – это и есть первая формулировка критерия Михайлова.

Если есть m неустойчивых корней, то приращение аргумента:

Δ arg D(jω) = (n-m)π –mπ =(n –2m) π

-∞ ≤ ω ≤ ∞

Разложим многочлен на действительную и мнимую части:

D(jω) = U(ω) + jV(ω)

U(ω) = b_n - b_n-2ω² +b_n-4ω⁴-…

V(ω) = b_n-1ω – b_n-3ω³ + b_n-5ω⁵-…

Оказывается действительная часть это четная функция: U(ω) = U(-ω),

а мнимая – нечетная: V(ω) = -V(ω).

Поэтому годограф многочлена описывает симметричную относительно оси абсцисс кривую:

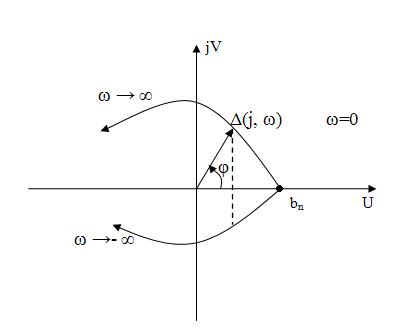
0 ≤ ω ≤ ∞

2-я формулировка критерия Михайлова: система будет устойчива, если при возрастании ω от 0 до ∞ вектор D(jω) повернётся на угол 0,5 nπ.

Δ arg D(jω) = 0,5[(n-m)π –mπ] =0,5(n –2m) π

0 ≤ ω ≤ ∞

3-я формулировка критерия Михайлова: для обеспечения устойчивости необходимо и достаточно выполнение следующих условий:

a) U(0) = b_n > 0

б) V′(0) = dV/dω = b_n-1 > 0

в) Все корни уравнений: U(ω) = 0 и V(ω) = 0 действительные и перемежающиеся, т.е. между двумя соседними корнями V(ω) = 0 лежит один корень уравнения: U(ω) = 0.

Для того, чтобы аргумент годографа набрал 0,5nπ для устойчивой системы при его вращении, т.е. при изменении ω от 0 до ∞, он должен начать движение из точки, расположенной правее 0 (b_n > 0), и вращаться против часовой стрелки (в положительном направлении) (dV/dω = b_n-1 > 0) последовательно проходя все квадранты комплексной плоскости, пересекая по очереди все оси (корни U(ω) = 0 и V(ω) = 0 действительные и перемежающиеся).

Пример перемежаемости корней:

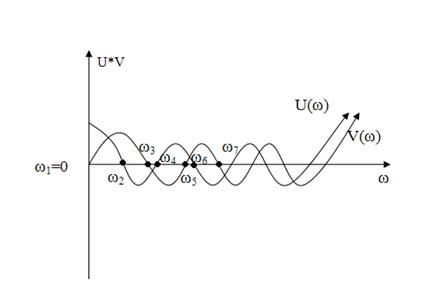
Существование комплексных корней уравнения, либо отсутствие перемежаемости свидетельствуют о неустойчивости системы. Поскольку для анализа устойчивости достаточно рассмотреть их поведение при изменении ω от 0 до ∞, то следует ограничиться определением неотрицательных корней уравнения.

Пример из домашнего задания

Задан характеристический многочлен:

D(p) = a₀p⁵ + a₁p⁴ + a₂p³ + a₃p² + a₄p + a₅

p = jω; D(jω) = U(ω) + jV(ω)

U(ω) = a₁ω⁴ – a₃ω² + a₅

V(ω) = a₀ω⁵ – a₂ω³ + a₄ω

1) U (0) = a5 > 0

2) V’(0) = a4 > 0

3) Решаем уравнения: U (ω) = 0

V (ω) = 0

Первое уравнения: a₁ω⁴ – a₃ω² + a₅ = 0 второе: a₀ω⁵ – a₂ω³ + a₄ω = 0 – это биквадратные уравнения.

ω (a₀ω⁴ – a₂ω² + a₄) = 0 первый корень всегда ω₁ = 0

Делаем замену: x = ω² a₁x² – a₃x + a₅ = 0

Решаем квадратное уравнение:

Другое уравнение: a₀ω⁴ – a₂ω² + a₄ = 0

x = ω²

a₀x² – a₂x + a₄ = 0 – решаем его.

Строим график для определения перемежаемости корней.

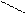
(U) ω₁ω₂ ω

(V) ω₁=0 ω₂

Пример из домашнего задания для критерия Найквиста

D(p) = a₀p⁵ + a₁p⁴ + a₂p³ + a₃p² + a₄p + a₅

p = jω; D(jω) = U(ω) + jV(ω)

U(ω) = a₁ω⁴ – a₃ω² + a₅

V(ω) = a₀ω⁵ – a₂ω³ + a₄ω

Рассчитываем таблицу, задавая значения ω:

ω U(ω) V(ω)

0.1

0.2

0.3

0.4

0.5

…

1

1.5

2.5

Строим годограф, и определяем, устойчива система или нет.

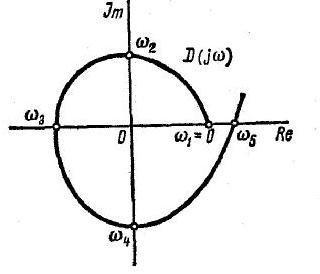
Если годограф не охватывает точку (-1; j0), то система устойчива (критерий Найквиста).

Дата добавления: 2014-01-11