Метод D – разбиения

Это метод синтеза устойчивой системы. Предложен Ю.И. Неймарком. Позволяет выделить область устойчивости в координатах выбранных параметров.

При некоторых фиксированных значениях коэффициента b_к характеристическое уравнение имеет вид:

_n

D (p) = ∑ b_kp^n-k = 0

^k=1

Будет m – неустойчивых и (n – m) – устойчивых корней.

При плавном изменении b_k корни будут перемещаться в плоскости корней, образуя траекторию.

Поясним это на примере: D(p) = в₀р³ + в₁р² + в₃ = 0

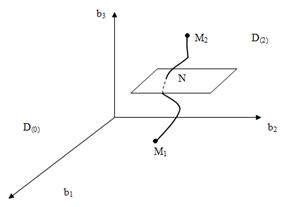
Рис. Пространство (коэффициентов) параметров

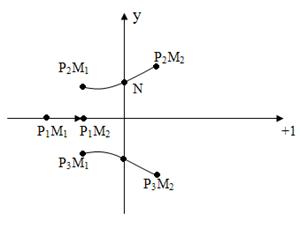
Рис. Перемещение корней в плоскости корней

Параметрам, лежащим на границе D – разбиения, соответствует характеристическое уравнение, имеющее хотя бы один корень на мнимой оси jω плоскости корней.

Совокупность коэффициентов b_kN, при которых хотя бы один корень или пара комплексных корней находится на мнимой оси, определяет поверхность N в пространстве коэффициентов. Таким образом, поверхность N делит пространство коэффициентов на области D(m) с числом корней m в правой полуплоскости и (n-m) – в левой. Такое разбиение пространства коэффициентов на области, соответствующие различному числу корней m в правой полуплоскости корней, называется D- разбиением. Граница D -разбиения в плоскости коэффициентов характеристического уравнения является отображением мнимой оси плоскости корней этого уравнения.

Аналогично с учетом связи коэффициентов уравнения с параметрами системы можно найти границу D -разбиения в координатах параметров.

Если в характеристическом уравнении заменить р на jω, то получим D(jω) = 0

Для каждого значения ω_k (корни этого уравнения) можно найти величины выделенных параметров, которые обращают в 0 левую часть уравнения. Эти значения параметров образуют точку, лежащую на границе D –разбиения.

Каждой точке границы D –разбиения соответствует определённое значение jω_k, являющееся корнем соответствующего характеристического уравнения.

D(jω) = U(ω) + jV(ω)

U(ω) = 0

V(ω) = 0

Зададим значение ω_k. Коэффициенты, удовлетворяющие этому значению образуют границу области D –разбиения.

Последовательно задавая значения ω от -∞ до +∞, построим всю границу D – разбиения.

D(p) = D₀(p) + П₁D₁(p) + П₂D₂(p) + … + П_k D_k(p), где D₀(p), D₁(p),…, D_k(p) – заданные полиномы (многочлены).

П₁, П₂, …, П_k – выделенные параметры системы.

В зависимости от числа выделенных параметров метод называют D – разбиение по 3–м параметрам (если их 3), по 2–м параметрам (если их 2) и по 1–му (если он 1).

++++++++++++++++++++++++++++++

Например, D – разбиение по 2 –параметрам.

D(p) = D₀(p) + П₁D₁(p) + П₂ D₂(p) = 0

Найдем значения П₁ и П₂, характеристическое уравнение имеет пару чисто мнимых корней p_1,2 = ±jω_i.

D(jω_i) = D₀(jω_i) + П₁D₁(jω_i) + П₂ D₂(jω_i) = 0

Разделим на 2 уравнения для действительной и мнимой частей:

П₂ Р₁(ω_i) + П₁Q₁(ω_i) = - R₁(ω_i)

П₂ Р₂(ω_i) + П₁Q₂(ω_i) = - R₂(ω_i)

где

P₁(ω_i) = Re D₂(jω_i); P₂(ω_i) = Im D₂(jω_i)

Q₁(ω_i) = Re D₁(jω_i); Q₂(ω_i) = Im D₁(jω_i)

R₁(ω_i) = Re D₀(jω_i); R₂(ω_i) = Im D₀(jω_i)

Решив систему относительно П₂ и П₁ с помощью правила Крамера, получим:

П₂ = ∆₂/∆; П₁ = ∆₁/∆ *

P₁(ω_i) Q₁(ω_i)

∆ =

P₂(ω_i) Q₂(ω_i)

-R₁(ω_i) Q₁(ω_i)

∆₂ =

-R₂(ω_i) Q₂(ω_i)

P₁(ω_i) -R₁(ω_i)

∆₁ =

P₂(ω_i) -R₂(ω_i)

Покажем, что главный определитель ∆ является нечетной функцией от ω.

Действительные части:

P₁(-ω) = P₁(ω) Q₁(-ω) = Q₁(ω)

Мнимые части:

P₂(-ω) = -P₂(ω) Q₂(-ω) = -Q₂(ω)

Аналогично можно показать, что определители ∆₁ и ∆₂ – нечетные функции от ω.

∆₁(ω) = - ∆₁(- ω)

∆₂(ω) = - ∆₂(ω)

Соответственно,

П₁(ω) = П₁(-ω) **

П₂(ω) = П₂(-ω)

четные функции

Уравнения *при изменении ω_i от -∞ до +∞ определяет кривую D-разбиения на участке П₂ П₁

Условия ** показывают, что каждой точке кривой D-разбиения соответствует пара корней P_{i, i+1} = ±jω_i, и что кривые D-разбиения при изменении ω от -∞ до ∞ накладываются друг на друга. Поэтому можно ограничиться изменением ω от 0 до ∞.

Особые прямые:

1) Прохождению значения через ∆ = 0 соответствует двум случаям:

Конечны и ∆₁ и ∆₂ ≠ 0, тогда:

П₁ и П₂ →∞

2) при ∆ = 0 значения ∆₁ = ∆₂ = 0 (уравнения*** не является линейно независимыми и их коэффициенты пропорциональны P₁(ω_i)/ P₂(ω_i) = Q₁(ω_i)/ Q₂(ω_i) = =R₁(ω_i)/ R₂(ω_i)). Тогда одно уравнение является следствием другого, т.е. вместо двух уравнений можно записать одно:

П₂P₁(ω_i) + П₁Q₁(ω_i) = - R₁(ω_i).

Это уравнение определяет в плоскости П₂, П₁ для некоторого фиксированного значения ∆ = ∆₁ = ∆₂ = ω_i положение линии, называемой особой прямой. Чтобы найти особые прямые, надо определить все значения ω_i, при которых одновременно

∆ = ∆₁ = ∆₂ = 0.

В частности, таким значением всегда является ω = 0, поскольку ∆, ∆₁, ∆₂ являются нечетными функциями ω и, следовательно, проходят через нуль при ω = 0. Тот же результат можно получить непосредственно из уравнения:

D₀(jω_i) + П₁D₁(jω_i) + П₂ D₂(jω_i) = 0, (1)

Положив в нем ω = 0 и записав q = 0.

Если коэффициент a_n не зависит от параметров П₂, П₁, то равенство (1) при ω = 0 записывается как

П₂*0 + П₁*0 = - a_n,

Оно не может осуществиться при конечных значениях П₂, П₁, т.е. особая прямая вся проходит в бесконечности и не представляет интереса.

Если в уравнении D(p) = D₀(p) + П₁D₁(p) + П₂ D₂(p) = 0 заменить переменную p = 1/q (при этом точка jω = ∞ отображается в точку q = 0), то вместо полинома D(p) со свободным членом a_n получим новый полином D(q) со свободным членом a₀. Следовательно, если a₀ не зависит от П₂, П₁, условие то a₀= 0 будет соответствовать особой прямой при ω = ∞. Если a₀ не зависит от П₂, П₁, то как и ранее, особая прямая проходит в бесконечности и не представляет интереса.

Таким образом, чтобы получить особые прямые, необходимо:

1) приравнять нулю a₀, если оно не зависит от параметров П₂, П₁, и получить уравнение особой прямой, соответствующей ω = ∞;

2) приравнять нулю a_n, если оно не зависит от параметров П₂, П₁, и получить уравнение особой прямой, соответствующей ω = 0;

3) найти все отличные от нуля значения ω, при которых одновременно обращаются в нуль детерминанты ∆, ∆₁, ∆₂. Подставив эти значения ω в уравнение

П₂P₁(ω_i) + П₁Q₁(ω_i) = - R₁(ω_i)

получим уравнения соответствующих особых прямых.

Штриховка границ D – разбиения.

Кривая D-разбиения при обходе в сторону возрастающих ω от -∞ до +∞ штрихуется слева, если ∆ > 0, и справа, если ∆ < 0.

Так как при изменении знака ω и ∆ меняет знак, то при двухкратном обходе кривой она оказывается два раза заштрихованной с одной стороны. Поэтому достаточно обходить при ω от 0 до +∞.

Штриховка особых прямых. Правила штриховки можно найти в учебниках.

Пересечение границы D-разбиения по направлению двойной штриховки соответствует переход из правой в левую полуплоскость 2-х сопряжённых корней. (новые значения - устойчивые корни).

Чтобы определить количество неустойчивых корней m (в правой полуплоскости) можно воспользоваться критериями Гурвица и Михайлова.

Пример из домашнего задания

Метод D – разбиения.

D(p) = a₀p⁵ + a₁p⁴ + a₂p³ + a₃p² + a₄p + a₅

D(p) = a₀p⁵ + a₁p⁴ + a₂p³ + a₃p² (1 + k₂) + a₄p (1 + k₁) + a₅ = 0

k₂D₂(p) + k₁D₁(p) + D₀(p) = 0

D₂ = a₃p²; D₁ = a₄p; D₀ = a₀p⁵ + а₁р⁴ + а₂р³ + а₃р² + а₄р + а₅

Подставим р = jω и разделим на действительные и мнимые части.

k₂a₃ω² + k₁*0+ a₁ω⁴ – a₃ω² + a₅ = 0

k₂*0 + k₁a₄ω + a₀ω⁵ – a₂ω³ + a₄ω = 0

k₁ = ∆₁/∆; k₂ = ∆₂/∆

-a₃ω² 0 -a₁ω⁴ + a₃ω² – a₅ 0

∆ =; ∆₂=

0 a₄ω -a₀ω⁵ + a₂ω³ – a₄ω a₄ω

-a₃ω² – a₁ω⁴ + a₃ω² -a₅

∆₁ =

0 -a₀ω⁵ + a₂ω³ – a₄ω

Вычислим k₁ и k₂, изменяя ω от 0 до ∞

ω k₁ k₂

0,1

0,2

0,3

…

1,5

Решения уравнений:

k₁ = (- а₀/а₄ )ω⁴ + (а₂/а₄ )ω² – 1

k₂ = -(а₁/а₃ )ω² - а₅/(а₃ω²) + 1

При k₁ = k₂ = 0 имеем исходное дисперсионное уравнение, оно по критерию Рауса – Гурвица имело m неустойчивых корней.

При обходе границы в сторону возрастающих ω (-∞; +∞) кривая D разбиения штрихуется слева, если главный определитель ∆ > 0, и справа, если ∆ < 0. Так как при изменении знака ω и ∆ меняет свой знак, то при 2-х кратном обходе кривой она оказывается дважды заштрихованной с одной и той же стороны.

Пересечения границы D – разбиения в точке ω_i по направлению штриховки соответствует переходу из правой в левую полуплоскость 2-х сопряжённых корней_i через мнимую ось комплексной плоскости корней.

Дата добавления: 2014-01-11