Модель одномерного объекта

МАТЕМАТИЧЕСКИЕ МОДЕЛИ И ОПТИМИЗАЦИЯ ПРОЦЕССОВ

Практикум

Given

5x1×x2+0.2x2=-6

-6x1+4x1×x2=0.8

При записи системы используется не знак равенства, а знак логического равенства =, который имеется на панели Булево. Затем вводится встроенная функция: r:=find(x1,x2)

Чтобы получить значения корней, надо записать: r=

1. Составить программу решения системы линейных уравнений по методу Гаусса. Коэффициенты системы даны в табл.24.1. Номер варианта определяет преподаватель

2. Решить эту же систему с помощью приложений Mathcad и Excel. Результаты сравнить между собой.

3. Решить систему нелинейных уравнений, приведенную выше, в приложении Mathcad.

Таблица 24.1

№	а11	а12	а13	а21	а22	а23	а31	а32	а33	b1	b2	b3
		-3				-2		-1		1,2	1,3	1,4
		-2			-4	-1		-1		1,7	1,6	1,9
			-1		-5			-3		6,2	2,4	1,8
			-1					-1	-4	2,3	1,4	1,7
		0,3	0,1	0,2		0,8	0,4	0,4		7,2	8,3	6,6
		0,6	-1	0,8		1,2		0,8	2,6	0,2	-3	2,7
		0,1	0,1	0,2		0,3	0,3	0,4		1,5	1,6	1,7
		1,2		1,5	2,8	0,7		1,5	3,5	7,1	7,7	4,2
	2,1	-2	0,3	0,7	1,9	0,6	0,3	0,7	1,5	1,6	0,9	3,5
	3,1	-2	0,5	0,8	2,7	-1	0,5	-1	2,1	1,3		2,3
	0,1	0,3	0,4	0,2	0,1	0,6	0,4	0,2	0,3	0,7	0,5	0,6
		-1			-5				-8	1,8	2,5	0,3
	7,1	-2	0,7	0,7	3,5	8,4	5,5	5,6	1,3	7,7	0,1	4,5
	2,5	0,2	0,1	0,1		0,4	0,2	0,2		3,6	4,2	3,3
	1,6	0,7	0,2	0,1	-2	0,5		0,2	2,5	1,9	2,6	2,3

Объект

Пусть в результате проведения эксперимента получена табличная зависимость значений выходного параметра процесса y от значений входного параметра x:

xy

Рис. 25.1 − Одномерный объект

Требуется получить эмпирическую формулу, описывающую зависимость y от x. Решение такой задачи состоит из двух этапов.

На первом этапе выбирается общий вид формулы, исходя из теоретических представлений о характере изучаемого процесса. Это может быть, например, полином m -степени:

y=a0+a1×x+a2×x²+…+am×x^m.

Формула может содержать тригонометрические, экспоненциальные, логарифмические функции и т.п.

На втором этапе определяются значения параметров a0,a1,a2,…,am эмпирической формулы f(x,a0,a1,a2,…am), которые обеспечивали бы соответствие этой формулы экспериментальным данным.

В соответствии с методом наименьших квадратов параметры a0,a1,a2,…,am выбираются так, чтобы была минимальной сумма квадратов:

(25.1)

Чтобы найти нужные параметры, следует взять частные производные от правой части (25.1) по a0,a1,a2,…,am и приравнять их нулю. Полученную систему уравнений можно решить одним из известных методов.

Пример. Пусть требуется определить параметры a0,a1,a2 формулы

y=a0+a1×x+a2×x² (25.2)

Выражение (25.1) будет тогда иметь вид:

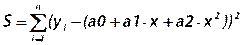
Далее берутся частные производные и приравниваются нулю:

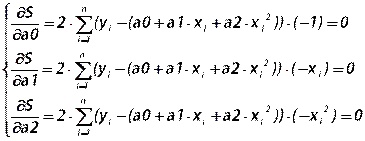
Отсюда

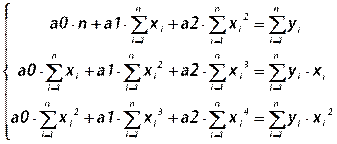(25.3)

Решив систему (25.3) можно определить искомые величины a0, a1, a2.

Алгоритм метода наименьших квадратов для эмпирической формулы (25.2)

1. Ввод количества опытов n, значений x₁, x₂,…x_n, y_1, y₂,…y_n.

2. Определение коэффициентов системы уравнений (21.3):

a_1,2=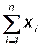, a_1,3=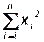, a_2,3=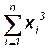, a_3,3= ,

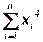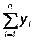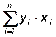b₁= , b₂= , b₃= ;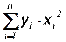

a_1,1=n, a_2,1= a_1,2, a_2,2= a_1,3, a_3,1= a_1,3, a_3,2= a_2,3.

3. Решение системы (25.3) A×Z=B, где A – матрица коэффициентов, B – вектор свободных членов системы, Z – вектор, в котором определяются корни z₁=a0, z₂=a1, z₃=a2.

4. Вывод искомых коэффициентов a0, a1, a2.

5. Определение и вывод разностей d₁, d₂,…d_n.

Дата добавления: 2014-01-20