Модель многомерного объекта

Получение математических моделей в приложениях Mathcad и Excel

В приложении Mathcad можно записать формулы приведенного выше алгоритма и вычислить коэффициенты функциональной зависимости.

Имеются также и встроенные функции для определения математических моделей. Например, пусть имеются значения х и у, полученные в результате проведения опытов. Надо найти математическую модель в виде полинома второй степени y=a0+a1×x+a2×x²

Можно использовать для решения задачи встроенную функцию linfit. На листе Mathcad тогда нужно записать:

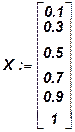
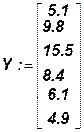
А:=linfit(Х, Y, F)

Вычисленные значения a0,a1,a2 будут записаны в векторе А, который появится после ввода текста: A=

Для построения графика теперь можно определить значения:

i:=0..5 t:=0,0.01..1 Z(t):=F(t)*A

Здесь Z(t) − искомая математическая модель. Если построить на одном графике зависимость Z(t) от t и зависимость Y_i от X_i, то можно сравнить, насколько хорошо полученный полином описывает данные опытов.

В приложении Excel имеется интересная возможность получения математических моделей через построение графиков функций.

Пусть имеются значения x₁, x₂,…x_n и соответствующие им значения y₁, y₂,…y_n. Надо для этих данных построить точечный график и выполнить Диаграмма/Добавить линию тренда. В появившемся окне на вкладке Тип определить вид математической модели, а на вкладке Параметры отметить флажок Показывать уравнение на диаграмме. После нажатия ОК искомое уравнение появится на графике.

Предположим, что технологический процесс можно описать математической моделью вида

y=b₀+b₁×x₁+…+b_n×x_n+b₁₂×x₁×x₂+…+b_n-1,n×x_n-1×x_n, (25.4)

где y – выходной параметр процесса; b₀,b₁, …,b_n-1,n –искомые неизвестные коэффициенты процесса; x₁,…,x_n – входные параметры процесса. Соотношения такого вида называются уравнениями регрессии.

Например, для процесса (рис. 25.2), имеющего три входных параметра (фактора) уравнение (25.4) примет вид:

y=b₀+b₁× x₁+b₂× x₂+b₃× x₃+b₁₂×x₁× x₂+b₁₃× x₁× x₃+b₂₃× x₂× x₃ (25.5)

Чтобы определить коэффициенты математической модели процесса необходимо провести эксперимент по соответствующему плану, например, по плану полного факторного эксперимента. Количество опытов в эксперименте определяется по формуле N=2ⁿ, где n – количество факторов. Входные воздействия принимают минимальные и максимальные значения. Для упрощения вычислений нужно перейти от физических переменных x₁,… x_n к кодированным по формуле:

z_i = 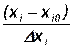, i=1,2,3 (25.6)

Здесь x_i0 – значение фактора на базовом (нулевом) уровне, равное среднему значению между минимальным и максимальным значениями; ∆x_i – интервал варьирования по данному фактору.

В случае трех входных параметров план проведения эксперимента имеет вид, представленный на рис. 25.3. Значение –1 соответствует минимальному значению входного параметра, +1 соответствует максимальному значению входного параметра.

В соответствии с методом наименьших квадратов производится вычисление коэффициентов:

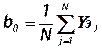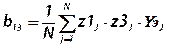, , , , , , , i=1,2,…,N (25.7)

Коэффициент регрессии b (b₀, b₁, … и т.д.) считается значимым, если выполняется условие

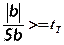, , (25.8)

где Sb – среднеквадратичная ошибка в определении коэффициентов регрессии; t_Т – табличное значение критерия Стьюдента, которое выбирается для числа степеней свободы f1=m-1.

Для расчета дисперсии воспроизводимости нужно выполнить дополнительно m опытов (m<N) по любой строчке плана, например, при значениях входных факторов на базовом уровне. В результате получаются дополнительные значения экспериментальных данных y_1д, y_1д, …,y_mд. Тогда

Sy²=, yoc=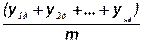, k=1,…,m

В табл.25.1 приведены значения критерия Стьюдента.

Таблица 25.1

Число степеней свободы f1
	12,71	4,30	3,18	2,78	2,57	2,45	2,36

В случае невыполнения условия (25.8) соответствующий коэффициент считается незначимым и приравнивается нулю.

Проверка адекватности (соответствия) полученного уравнения регрессии экспериментальным данным проводится с помощью критерия Фишера. Для этого вычисляются

, F= ,

где – оценка дисперсии адекватности; B – число значимых коэффициентов уравнения регрессии; yэ_j, yp_j – экспериментальное и рассчитанное по уравнению (25.5) значение y в j -ом опыте.

Определяется также табличное значение критерия Фишера F_Т из таблицы по числу степеней свободы f1 и числу степеней свободы f2=N-B.

Если F<F_Т, то уравнение регрессии рассматривается как модель исследуемого процесса.

В табл. 25.2 приведены коэффициенты критерия Фишера.

Таблица 25.2

Число степеней свободы f1	Число степеней свободы f2
	161,40	199,50	215,70	224.60	320,20	234,00
	18,51	19,00	19,16	19,25	19,30	19,33
	10,13	9,55	9,28	9,12	9,01	8,94
	7,71	6,94	6,59	6,39	6,26	6,16
	6,61	5,79	5,41	5,19	5,05	4,95
	5,99	5,14	4,76	4,53	3,39	4,28
	5,99	4,74	4,35	4,12	3,97	3,97

Если полученное уравнение не адекватно процессу, то нужно перейти к более сложному виду математической модели, вновь провести опыты и обработать их результаты. Если уравнение адекватно процессу, то нужно от кодированных переменных перейти к физическим по формуле (25.6).

Дата добавления: 2014-01-20