Двухмодальные распределения

К ним относятся дискретное двузначное, арксинусоидальное и двухмодальные остро– и кругловершинные распределения.

Дискретное двузначное распределение – это распределение, при котором с равными вероятностями встречаются только два значения случайной величины. В центрированном виде (рис. 5.6) оно описывается формулой

,

где δ(х) – дельта-функция Дирака; ±А – возможные значения случайной величины.

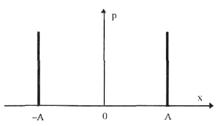
Рисунок 5.6 – Дискретное двузначное распределение

При дискретном дву­значном распределении СКО равно значению пара­метра А, ε = 1, к = 1.

Дискретное двузнач­ное распределение может быть приближенно пред­ставлено в виде суммы двух нормальных распределений с одинаковыми по модулю, но противо­положными по знаку m_х и при стремлении к нулю их СКО:

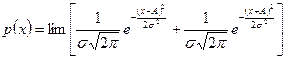
Остро– и кругловершинные двухмодальные распределения по­лучаются как композиция дискретного двузначного и экспоненци­ального распределений с различными значениями коэффициента а (рис. 5.7). При α < 2 получаются островершинные, при α > 2 – кругловершинные распределения.

Основными параметрами таких распределений являются:

• показатель относительного содержания в композиции дискрет­ной составляющей

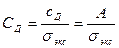
где σ_д и σ_экс – СКО дискрет­ного и экспоненциального распределений. Как правило, С_Д (0; 2).

Чем больше показатель С_д, тем больше провал. При С_д = 0 провал на графике распределения отсутствует;

• показатель степени а для экспоненциальных распределений, который обычно лежит в пределах от 0,5 до 2.

Островершинные распределения получаются при использовании некоторых высокоточных цифровых вольтметров, а кругловершинные распределения имеют погрешности от механического гистере­зиса элементов приборов и датчиков.

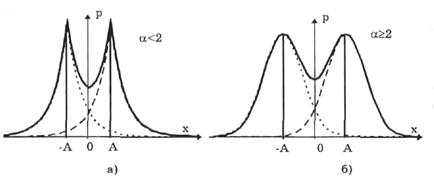
Рисунок 5.7 – Островершинные (а) и кругловершинные (б) двухмодальные распределения

Дата добавления: 2014-01-20