Теорема Абеля

Если степенной ряд 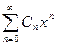сходится в точке 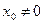, то он сходится и притом абсолютно в интервале 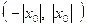, то есть при всех значениях 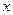, удовлетворяющих условию. .

Следствие:

Если степенной ряд расходится при некотором значении 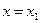, то он расходится и при всех значениях .

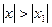Любой степенной ряд сходится при значении 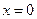. Естьстепенныеряды, которые сходятся только при 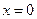и расходятся приостальныхзначениях .

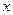Область сходимости может состоять из всех точекоси Ох, другимисловами, ряд может сходится при всех .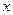

Пример 39 Исследовать сходимость ряда .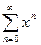

Решение:

Ряд 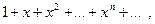представляет геометрическую прогрессию со знаменателем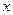, сходится при 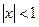и расходитсяпри .

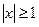Из теоремы Абеля и ее следствия получаем, что все точки сходимости расположены от начала координат не дальше, чем любая из точек расходимости. Совершенно ясно, что точки сходимости будут целиком заполнять некоторый интервал с центром в начале координат.

Таким образом, можно сказать, что для каждого степенного ряда, имеющего как точки сходимости, так и точки расходимости, существует такое положительное число 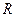, что для всех 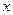, по модулю меньших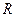 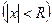, ряд абсолютно сходится, а для всех 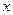, по модулю больших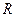 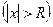, ряд расходится.

Что касается значений 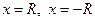здесь могут быть различные возможности: ряд может сходится в обеих точках, или только в одной из них, или ни в одной. При этом ряд может сходиться как абсолютно, так и условно.

Радиусом сходимости степенного ряда 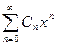называетсятакое число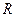, что для всех 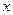, , 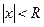степенной ряд сходится, а для всех 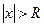, расходится. Интервал 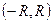называется интервалом сходимости.

Условимся для рядов, расходящихся при всех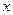, кроме 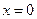. считать 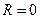, а для рядов, сходящихся при всех 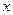, считать .

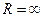Как найти радиус сходимости?

Если все коэффициенты степенного ряда, начиная с некоторого, отличны от нуля, то его радиус сходимости равен пределу при 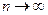отношения абсолютных величин коэффициентов общего и следующего за ним членов ряда.

Составим ряд из абсолютных величин членов ряда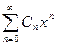

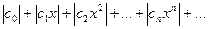
Найдем отношение 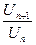для этого ряда:

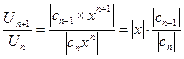
а затем предел его при :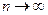

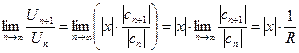
Здесь множитель 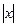вынесен за знак предела, как не зависящий от 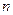и введено обозначение

,

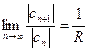если этот предел существует и не равен нулю. Согласно признаку Даламбера, ряд сходится, если 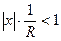,. откуда 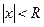. Отсюда следует, что ряд сходится, и притом абсолютно, при значениях .

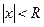Согласно томуже признаку Даламбера, ряд расходится, ес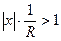ли или 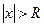. Однако в этом случае из признака Даламбера следует, что члены ряда не стремятся к нулю. Тогда при 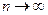не стремятся к нулю и члены ряда, а потому и он расходится при значениях 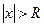. Следовательно, согласно определению, число 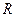– радиус сходимости степенного ряда. из соотношения получим

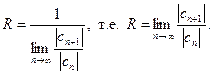
Пример 40 Найти радиус сходимости ряда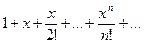

Решение:

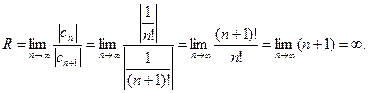
Пример 41 Найти область сходимости степенного ряда

Решение:

Найдем отношение

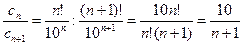
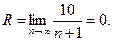т. е. ряд сходится только при 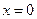и расходится при остальных значениях .

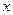Пример 42 Найти область сходимости степенного ряда:

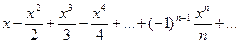
Решение:

Здесь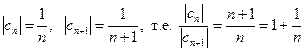

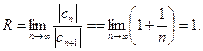
Исследуем сходимость ряда на концах интервала сходимости.

При 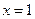имеем ряд 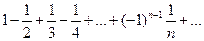он сходится по теореме Лейбница.

При 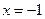имеем ряд 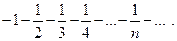, который расходится как произведение расходящегося гармонического ряда на -1. Следовательно; областью сходимости служит полуинтервал .

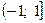Пример 43 Найти область сходимости степенного ряда

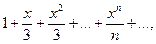
Решение:

Найдем радиус сходимости ряда

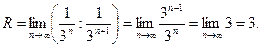
Исследуем сходимость ряда при значениях 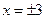. Подставив их в данный ряд соответственно получим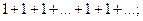

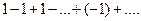Оба ряда расходятся, так как не выполняется необходимое условие сходимости (их общие члены не стремятся к нулю при 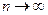). На обоих концах интервала сходимости данный ряд расходится а область его сходимости

Замечание.

Формула радиуса сходимости степенного ряда получена в предположении, что все коэффициенты членов ряда начиная с некоторого, отличны от нуля. Применение формулы допустимо только в этих случаях. Если это условие нарушается, то радиус сходимости степенного ряда следует искать или с помощью признаков Даламбера. Коши, или же сделав замену переменной, преобразованием ряда к виду в котором указанное условие выполняется.

Дата добавления: 2014-01-11