Множество R

Перечислим основные свойства, которыми обладают действия над действительными числами. Множество всех действительных чисел будем обозначать через R, а его подмножества будем называть числовыми множествами.

1. Операции сложения. Для любой пары действительных чисел a и b определено единственное число, называемое их суммой и обозначаемой 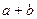, так, что при этом выполняются следующие условия:

1.1 .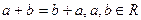

1.2 .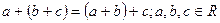

1.3 Существует такое число, называемое нулем и обозначаемое 0, что .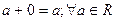

1.4 Для любого числа 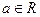существует число, называемое ему противоположным и обозначаемое – а, для которого 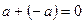. Число 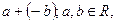называется разностью чисел a и b и обозначается .

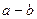2. Операция умножения. Для любой пары действительных чисел a и b определено единственное число, называемое их произведением и обозначаемой 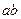, так, что при этом выполняются следующие условия:

2.1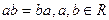

2.2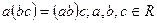

2.3 Существует такое число, называемое единицей и обозначаемое 1, что .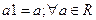

2.4 Для любого числа 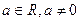существует число, называемое ему обратным и обозначаемое 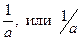, для которого 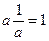. Число 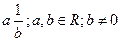, называется частным от деления a на b и обозначается .

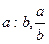3. Связь операций сложения и умножения.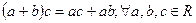

4. Упорядоченность. Для действительных чисел определено отношение порядка. Оно состоит в следующем. Для любых двух различных чисел a и b имеет место одно из двух соотношений: либо a<b, либо a>b. При этом предполагается, что выполняются следующие условия:

4.1 Транзитивность. Если a<b и b<c, то a<c.

4.2 Если a<b, то для любого числа с имеет место a+c<b+c.

4.3 Если a>b, c>0, то ac>bc.

Из выполнения условий 4.2. и 4.3 вытекает одно важное свойство, называемое плотностью действительных чисел.: для любых двух различных действительных чисел 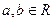(например, 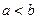) существует такое число с, что .

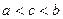5. Множество действительных чисел обладает еще и свойством непрерывности. Для любых непустых числовых множеств X и Y таких, что для каждой пары чисел xÎ X, yÎ Y выполняется неравенство 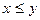, существует число а, удовлетворяющее условию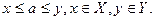

Перечисленные свойства полностью определяют множество действительных чисел в том смысле, что из этих свойств следуют и все остальные его свойства. Поэтому можно дать аксиоматическое определение множества действительных чисел следующим образом.

Определение 1 Множество элементов, обладающих свойствами 1- 5, содержащее более одного элемента, называется множеством действительных чисел, а каждый его элемент – действительным числом.

Дата добавления: 2014-01-20