Некоторые предварительные понятия

Задача об устойчивости сжатого стрежня

ОСНОВЫ ЧИСЛЕННЫХ МЕТОДОВ

Лекция-2

Наиболее сложным и достаточно частым видом разрушений конструкции является, так называемая, потеря устойчивости. В курсе сопротивления материалов, как правило, дается математическая формулировка задачи устойчивости стержня (3.2.1), которая представляется следующей расчетной схемой (рис. 3.2.1):

Рис. 3.2.1. К задаче об устойчивости сжатого стержня.

При действии достаточно небольшой сжимающей силы 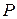на статически определимую балку, ее прогиб равен нулю. Возникает вопрос, существует ли величина силы 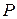, вызывающая изгиб стержня. Если существует, то она удовлетворяет условиям

(3.2.1)

где 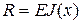– жесткость балк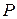и; и – искомые величины.

В курсе строительной механики величина 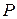, при которой , называется критической силой, а – формой потери устойчивости. В математической терминологии величина критической силы 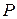называется собственным значением оператора краевой задачи (3.2.1), а – собственной функцией этого оператора.

Однако очевидно, что и при любом значении 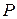прогиб является решением (3.2.1) (тривиальное решение).

Аналитическое решение данной задачи существует только при 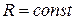, в остальных случая задача решается только численно, в частности, методом конечным разностей.

Дата добавления: 2014-01-20