Графический метод. Если матричная игра имеет размерность 2хn или mx2, то найти оптимальные смешанные стратегии можно графически

Если матричная игра имеет размерность 2хn или mx2, то найти оптимальные смешанные стратегии можно графически.

ДАНО. игра 2хn

a_ij– выигрыш игрока А при использовании им стратегии i, когда игрок В использует стратегию j

НАЙТИ. v – цену игры.

(х₁*, х₂*) – вероятности использования игроком А соответственно 1 и 2 стратегий

(y₁*, y₂*, …y_n*) – вероятности использования игроком В своих стратегий.

РЕШЕНИЕ, х₁ +х₂ =1, 0£x£1.

Выигрыш игрока А при применении противником чистой стратегии В_i составит z_i:

z₁= a₁₁х₁ +a₂₁х₂= a₁₁х₁ +a₂₁ (1–х₁)=(a₁₁ –a₂₁) х₁ +a₂₁

z₂= a₁₂х₁ +a₂₂х₂= a₁₂х₁ +a₂₂ (1–х₁)=(a₁₂–a₂₂) х₁ +a₂₂

…

z_n= a_1nх₁ +a_2nх₂= a_1nх₁ +a_2n (1–х₁)=(a_1n–a_2n) х₁ +a_2n

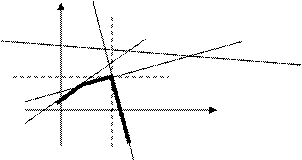Построим на плоскости прямые z_i(x₁).

z

z*

х* 1 x₁

Нижняя огибающая этих прямых – это минимальный гарантированный выигрыш игрока А. Действуя по принципу «минимакса», найдем точку на этой огибающей с максимальным выигрышем (х*, z*). Тогда v=z*, (х₁*, х₂*) =(х*, 1-х*)

Нижняя огибающая является наилучшим вариантом для игрока В (проиграть как можно меньше). Худший для него случай – точка (х*, z*). Эта точка является точкой пересечения прямых, соответствующих k и l стратегиям игрока В. Эти стратегии и являются оптимальными смешанными для него. Вероятность использования остальных стратегий y_i=0

При использовании игроком В пары оптимальных смешанных стратегий выигрыш игрока А будет не больше цены игры. В наилучшем случае для любой стратегии =v, т.е. a_1ky_k +a_1l y_l= a_2ky_k +a_2l y_l

Т.к. 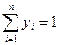, то y_l =1–y_k. Решив уравнение, найдем y_k

ПРИМЕР 5.4.

	В1	В2	В3
A1	2	-3	4
A2	-3	4	-5

z₁= 2х₁ -3х₂= 2х₁ -3 (1–х₁)=5 х₁ –3

z₂= -3х₁ +4х₂=-3х₁ +4 (1–х₁)=-7 х₁ +4

z₃= 4х₁ -5х₂=4х₁ -5 (1–х₁)=9 х₁ –5

x₁

x₃ x₂

z₁=z₂ 5 х₁ –3=-7 х₁ +4 12 х₁=7 х₁*=7/12 x₂*=5/12 v=z*=-1/12

y₃=0 2y₁–3y₂=-3y₁+4y₂ 5y₁-3=-7y₁+4 12y₁=7 y₁*=7/12 y₂*=5/12

Ответ: х*=(7/12, 5/12) y*=(7/12, 5/12, 0) v=-1/12

Дата добавления: 2014-01-20