Игры с природой

В играх с природой оптимальную стратегию выбирает только одна сторона, со стороны природы противодействие отсутствует.

Существует ряд критериев для выбора решения в играх с природой.

1. Максиминный критерий Вальда. Согласно этому критерию игра с природой ведется как игра с разумным, причем агрессивным противником, делающим все для того, чтобы помешать нам достигнуть успеха. Оптимальной считается стратегия, при которой гарантируется выигрыш в любом случае не меньший, чем «нижняя цена игры с природой»: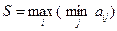

Если руководствоваться этим критерием, олицетворяющим «позицию крайнего пессимизма», надо всегда ориентироваться на худшие условия, зная наверняка, что «хуже этого не будет». Очевидно, такой подход — «перестраховочный», естественный для того, кто очень боится проиграть,— не является единственно возможным, но как крайний случай он заслуживает рассмотрения.

2. Критерий минимаксного риска Сэвиджа. Этот критерий — тоже крайне пессимистический, но при выборе оптимальной стратегии советует ориентироваться не на выигрыш, а на риск. Выбирается в качестве оптимальной та стратегия, при которой величина риска в наихудших условиях минимальна: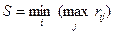

Сущность такого подхода в том, чтобы всячески избегать большого риска при принятии решения. В смысле «пессимизма» критерий Сэвиджа сходен с критерием Вальда, но самый «пессимизм» здесь понимается по-другому.

Риском r_ij игрока А при пользовании стратегией А_i в условиях П _j называется разность между выигрышем, который мы получили бы, если бы знали условия П _j, и выигрышем, который мы получим, не зная их и выбирая стратегию А_i

Пусть максимальный выигрыш в столбце – β_j, тогда r_ij=β_j-a_ij

3. Критерий пессимизма-оптимизма Гурвица. Этот критерий рекомендует при выборе решения не руководствоваться ни крайним пессимизмом («всегда рассчитывай на худшее!»), ни крайним, легкомысленным оптимизмом («авось кривая вывезет!»). Согласно этому критерию выбирается стратегия из условия: ,

где χ – «коэффициент пессимизма»: 0 ≤ χ ≤ 1 При χ=1 критерий Гурвица превращается в критерий Вальда, а при χ=0 в критерий «крайнего оптимизма». Коэффициент пессимизма выбирается из субъективных соображений: чем опаснее ситуация, тем χ ближе к 1.

ПРИМЕР 5.5. Бригада строителей вместе с семьями и обслуживающим персоналом живёт в посёлке недалеко от строительства. В связи с приближением зимы возникает проблема создания запасов угля. Если зима будет мягкая, потребуется 12 тонн угля, для нормальной – 15 тонн, а для суровой – 18 тонн. Стоимость тонны угля соответственно 10, 12, 14 у.е. В настоящее время уголь можно приобрести по 10 у.е. за тонну. Требуется создать наиболее подходящий запас угля на зиму.

Описанную ситуацию можно рассматривать как игру двух лиц: жителей посёлка и природы, каждый из которых имеет в своём распоряжении три выбора: 1 - купить 12, 15 или 18 тонн угля сейчас, а остальное потом; 2 – «выбрать» мягкую, нормальную или суровую зиму. Составим матрицу выигрышей этой игры, элементы которой обозначают у.е.:

Матрица игры:

	Мягкая	нормальная	холодная	min	max	c=0,5
	-120	-156	-204	-204	-120	-162
	-150	-150	-192	-192	-150	-171
	-180	-180	-180	-180	-180	-180
max	-120	-150	-180

Матрица риска:

	Мягкая	нормальная	холодная	mах

Задание 1. АО в апреле планирует пошив костюмов, причем костюм обходится ей по 20у.е. Реализация продукции происходит в мае по цене 40 у.е. По статистическим данным в мае в прохладную погоду можно продать 100 костюмов, в нормальную – 60, а в теплую – 30 костюмов. Как показала практика, товар, не реализованный в течение месяца, долго лежит на складе и дохода не приносит. Требуется изготовить такое количество товара, которое максимизирует доход АО.

Задание 2. Требуется продать ноутбук. Сейчас это можно сделать за 10 у.е. По стат. данным потом цена может возрасти на 10% или понизиться на 20%. Когда продавать, сейчас или подождать?

Раздел VI. ТЕОРИЯ МАССОВОГО ОБСЛУЖИВАНИЯ.

Дата добавления: 2014-01-20