Марковские случайные процессы

В физической системе S (техническое устройство, предприятие, живой организм) протекает случайный процесс, если она с течением времени меняет своё состояние, причём случайным образом.

ПРИМЕРЫ. Движение автобусов (задержка на остановках), летящий самолёт (изменения в атмосфере), конвейер (отказ узлов).

Случайные возмущения присущи любому процессу. Но пока эти возмущения несущественны, ими можно пренебречь и рассматривать процесс как детерминированный.

Случайный процесс, протекающей в системе, называется марковским, если для любого момента времени t₀ вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент t₀ и не зависят от того, когда и как система пришла в это состояние. В марковском процессе будущее зависит от прошлого только через настоящее. Любой процесс можно рассматривать как марковский, если параметры из прошлого, от которых зависит будущее, включить в настоящее.

ПРИМЕР. Система – техническое устройство. Если за настоящее состояние системы считать «система исправна», то это процесс не марковский, потому что вероятность дальнейшей безотказной работы зависит от прошлого (от того, сколько она уже проработала). Если же в настоящее состояние системы включить общее время работы и время последнего ремонта, то процесс можно считать марковским.

Процесс называется процессом с дискретными состояниями, если его возможные состояния можно заранее перечислить, и переход системы из состояния в состояние происходит практически мгновенно. Процесс называется процессом с непрерывным временем, если моменты возможных переходов из состояния в состояние случайны.

ПРИМЕР 6.1. Техническое устройство состоит из двух узлов. Время выхода из строя и время ремонта – случайны. Возможные состояния системы можно перечислить:

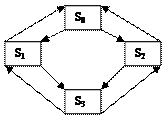S₀ – оба узла исправны;

S₁ – первый узел ремонтируется, второй – исправен;

S₂ – второй узел ремонтируется, первый – исправен;

S₃ – оба узла ремонтируются;

Граф состояний – это ориентированный граф, вершинами которого являются состояния, а дугами – возможные переходы из состояния в состояние.

Потоком событий называется последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени.

ПРИМЕРЫ. Поток вызовов на телефонной станции; поток пассажирского транспорта, подходящего к остановке.

Поток событий можно наглядно изобразить рядом точек на оси времени.

m₁ m₂ l₁ l₂ m ₂ l₂ l₁ m₁  

. 0 ............. t

Интенсивность l – это среднее число событий, приходящееся на единицу времени: l=1/t_з. Граф состояний, у которого для каждой дуги проставлена интенсивность того потока событий, который переводит систему по данной стрелке в другое состояние, называется размеченным.

Виды потоков событий:

регулярный, если события следуют одно за другим через равные промежутки времени;

стационарный, если вероятностные характеристики потока не зависят от времени;

без последействия, если для любых двух непересекающихся участков времени число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой;

ординарный, если события в нём появляются поодиночке;

простейший, если он стационарен, ординарен и не имеет последействия.

ПРИМЕРЫ. Поток заявок на телефонной станции в период с 13 до 14 практически стационарен. Однако его нельзя считать стационарным в течение суток.

Интенсивность стационарного потока постоянна. Это не значит, что число событий, появляющееся в единицу времени постоянно. Могут существовать сгущения и разрежения, носящие случайный характер.

Если все потоки событий, переводящие систему S из состояния в состояние, – простейшие, то процесс, протекающий в системе, будет марковским (в простейшем потоке «будущее» не зависит от «прошлого»).

Вероятностью i-ого состояния называется вероятность p_i(t) того, что в момент времени t система будет находиться в состоянии S_i.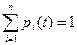

Все вероятности состояний как функции времени можно найти по размеченному графу состояний с помощью дифференциальных уравнений Колмогорова.

ПРАВИЛА СОСТАВЛЕНИЯ УРАВНЕНИЙ КОЛМОГОРОВА.

В левой части i-ого уравнения стоит производная вероятности i-ого состояния. В правой части – сумма произведений вероятностей всех состояний, из которых идут стрелки в данное состояние, на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного состояния.

ПРИМЕР 6.1.

m₁ m₂ l₁ l₂ m ₂ l₂ l₁ m₁  

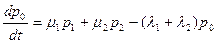
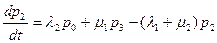
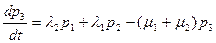
Чтобы решить уравнения Колмогорова и найти вероятности состояний, надо задать начальные условия. Если мы точно знаем начальное состояние системы S_i, то в начальный момент времени (при t=0) p_i(0)=1, а все остальные вероятности равны 0. Далее систему дифференциальных уравнений обычно решают численными методами с помощью ЭВМ.

Что будет происходить с вероятностями состояний при t® ∞? Если существуют какие-то пределы функций p_i(t) и они не зависят от начального состояния системы, то они называются финальными вероятностями состояний. lim p_i(t)= P_i

Финальную вероятность состояния можно истолковать как среднее относительное время пребывания системы в этом состоянии.

ТЕОРЕМА. Если число состояний системы конечно и из каждого из них можно перейти в любое другое (за конечное число шагов), то финальные вероятности существуют.

Если вероятности постоянны, то их производные равны 0. Тогда система уравнений Колмогорова превращается в систему линейных алгебраических уравнений.

ПРИМЕР 6.1.

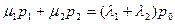
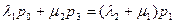
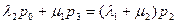
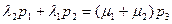
Уравнения системы однородны и, значит, определяют неизвестные только с точностью до произвольного множителя. Поэтому одно из уравнений заменим нормировочным условием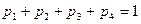

Зададимся численными значениями интенсивностей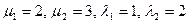

Решая систему, получим: p₀=6/15≈0.4; p₁=3/15≈0.2; p₂=4/15≈0.27; p₀=2/15≈0.13

Т.е. в предельном режиме система в среднем 40% времени будет проводить в состоянии S₀ (оба узла работают), 20% – в состоянии S₁, 27% – в состоянии S₂, 13% – в состоянии S₃(оба узла ремонтируются). Знание этих финальных вероятностей может помочь оценить среднюю эффективность работы системы и загрузку ремонтных органов.

Дата добавления: 2014-01-20