Формула Литтла

Схема гибели и размножения.

Задачи теории массового обслуживания.

СМО – система массового обслуживания, предназначенная для обслуживания какого-то потока заявок, поступающих в случайные моменты времени. Каждая СМО состоит из какого-то числа обслуживающих единиц, которые будем называть каналами обслуживания. Процесс работы СМО представляет собой случайный процесс с дискретными состояниями и непрерывным временем. Предмет теории массового обслуживания – построение математических моделей, связывающих заданные условия работы СМО (число каналов, их производительность, правила работы) с интересующими нас характеристиками – показателями эффективности, описывающими с различных точек зрения её способность справляться с потоком заявок.

Системы массового обслуживания делятся на типы по ряду признаков:

одноканальные и многоканальные (лифт и телефон);

с отказами и с очередью (телефон и парикмахерская);

открытые и замкнутые (магазин и группа станков, обслуживаемая одним рабочим).

СМО с очередью подразделяются на разные виды, в зависимости от того, как организована очередь – ограничена она или не ограничена. Ограничения могут касаться как длины очереди, так и времени ожидания. Такие СМО могут различаться и по дисциплине обслуживания. Заявки могут обслуживаться в порядке поступления, в случайном порядке, в приоритетном. Приоритет может быть как абсолютным, так и относительным.

В открытой СМО характеристики потока заявок не зависят от того, в каком состоянии сама СМО (сколько каналов занято), а в замкнутой – зависят.

Оптимизация работы СМО может производиться под разными углами зрения: с точки зрения владельца (предельно загрузить все каналы) или с точки зрения клиентов (уменьшить очереди). Задачи массового обслуживания являются многокритериальными.

Во многих случаях для принятия разумного решения по организации СМО достаточно приближённого ориентировочного знания её характеристик. Для этого может пригодиться аппарат простейшей марковской теории массового обслуживания.

Рассмотрим размеченный граф состояний схемы гибели и размножения.

λ₀₁ λ₁₂ λ₂₃ λ_k-1,k λ_k,k+1 λ_n-1

_,n

λ₁₀ λ₂₁ λ₃₂ λ_k,k-1 λ_k+1,k λ_n,n-1

Предположим, что потоки событий, переводящие систему по стрелкам графа простейшие. Из каждого состояния можно перейти в каждое другое и число состояний конечное, следовательно, существуют финальные вероятности. Составим систему уравнений Колмогорова.

S₀: λ₀₁p₀= λ₁₀p₁

S₁: (λ₁₂+ λ₁₀ ) p₁= λ₀₁p₀ +λ₂₁ p₂ →λ₁₂ p₁= λ₂₁ p₂

S_n-1: λ_{n-1 n} p_n-1= λ_{n n-1} p_n

Преобразуя эту систему уравнений, получим для любого k=1, 2,… n

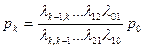
В числители стоит произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо (с начала и до данного состояния), а в знаменателе – произведение всех интенсивностей, стоящих у стрелок, ведущих справа налево.

Подставляя выражения для финальных вероятностей в нормировочное условие 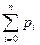=1, получим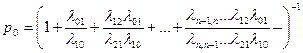

С любой СМО связаны два потока заявок: поток заявок, прибывающих в СМО, и поток заявок, её покидающих. Если в системе установился предельный стационарный режим, то среднее число прибывающих за единицу времени заявок равно среднему числу покидающих систему заявок, т.е. оба потока имеют одинаковую интенсивность λ.

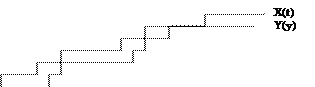
Пусть X(t) – число заявок прибывших в СМО до момента времени t, Y(t) – число заявок покинувших в СМО до момента t. Эти функции являются случайными и меняются скачком в момент прихода или ухода заявок.

t

Z(t)=X(t)-Y(t) – число заявок, находящихся в СМО. На большом промежутке времени Т среднее число заявок, находящихся в СМО может быть вычислено по формуле:

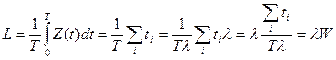
Интеграл равен суммарной площади прямоугольников, изображённых на графике. Высота этих прямоугольников =1, а основание равно времени пребывания в системе соответствующей заявки: t₁, t₂,… (при большом Т неважно, что последние прямоугольники войдут в сумму неполностью). Тλ – среднее число заявок, пришедшее за время Т.

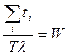– среднее время пребывания заявки в системе.

Получили формулу Литтла: для любой СМО, при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания среднее время пребывания заявки в системе равно среднему числу заявок в системе, делённому на интенсивность потока заявок: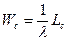

Среднее время пребывания заявки в очереди и среднее число заявок в очереди связано аналогичным образом: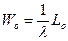

Дата добавления: 2014-01-20