Группировка данных. Вариационный ряд

Виды признаков

Генеральная совокупность и выборка

Вся подлежащая изучению совокупность однородных объектов называется генеральной совокупностью. Множество объектов, случайно отобранных из генеральной совокупности, называется выборкой. Число объектов в генеральной совокупности или в выборке называют их объемами (в дальнейшем, N – объем генеральной совокупности, n – объем выборки).

Для того, чтобы по данным выборки можно было достаточно уверенно судить об интересующем нас признаке генеральной совокупности, необходимо, чтобы свойства объектов выборки правильно отражали свойства объектов генеральной совокупности. Другими словами, выборка должна быть репрезентативной (представительной). Репрезентативность выборки достигается, если ее производят случайным образом (т.е. все объекты генеральной совокупности имеют одинаковую вероятность попасть в выборку).

Способы обработки данных зависят от характера исследуемого признака. Признаки делятся на качественные и количественные. Отдельные значения качественного признака выражаются понятиями, наименованиями, свойствами (цвет глаз, место работы и т.п.), количественного – числами (возраст, стаж работы, количество лепестков цветка и т.п.).

Количественный признак может быть дискретным и непрерывным. Дискретный признак принимает значения из некоторой конечной числовой последовательности, эти значения можно пронумеровать (число подтягиваний на перекладине, размер обуви, число позвонков у птиц). Признак, который может принимать любые значения из какого-либо числового промежутка, называется непрерывным (рост, длина стопы, масса яблока).

В дальнейшем будем использовать обозначения Х – изучаемый признак, х₁, х₂, …,х_к,.. – его значения, присущие членам совокупности, или варианты.

Первичным результатом статистического исследования является простой статистической ряд. Он представляет собой перечень членов совокупности и соответствующих им значений признака.

Пример 1. Собраны данные о результатах в беге на 100 метров, показанные группой школьников 10 класса. Результаты (в с) занесены в таблицу.

Таблица 1.

Школьник
Результат	16.2	15.4	15.5	14.5	14.3	16.6	16.8	15.3

Таблица 1 является простым статистическим рядом. Члены совокупности – школьники, варианты – результат в беге на 100 м.

Следующим шагом в изучении признака является группировка – разделение членов совокупности на группы, в которых члены совокупности принимают либо одни и те же значения, либо значения внутри определенного интервала. Способы группировки зависят от вида признака.

· Группировка данных качественного признака

Пример 2. При опросе туристической группы (20 человек) выяснено, что среди них 5 человек городские жители, 5 – сельские. Данные сгруппированы в Таблице 2.

Таблица 2.

Группировка туристов по месту жительства.

Туристы	городские	сельские	всего
Количество

· Для группировки данных в случае количественного дискретного признака располагают все варианты в порядке возрастания и указывают частоту, с которой они встречаются в данной совокупности.

Пример 3. Имеются данные об оценках 24 студентов, полученных ими на экзамене

Минимальное значение оценки х_min – 2, максимальное х_max – 5. Подсчитав частоту, с которой встречаются варианты, оформим таблицу (см. Таблицу 3).

Таблица 3.

хi	ni

Таблица, позволяющая судить о распределении частот между вариантами, называется дискретным вариационным рядом.

· Группировка данных в случае количественного непрерывного признака (или дискретного признака, когда число вариант велико).

В этом случае строят интервальный вариационный ряд. Для построения интервального вариационного рядя определяют величину (ширину) интервала, составляют шкалу интервалов и в соответствии с ней группируют результаты наблюдений. Для определения ширины интервала используют формулу: где h – ширина интервала, х_min и х_max – минимальная и максимальная варианты, k – число групп; или формулу Стэрджеса, позволяющую определить оптимальную величину интервала 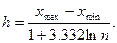Если h оказывается дробным числом, то за ширину интервала принимают либо ближайшее целое число, либо ближайшую несложную дробь. За начало первого интервала рекомендуется принимать величину, равную (х_min – h/2), второго интервала (x_min + h/2) и т.д. Построение интервалов продолжают до тех пор, пока начало следующего по порядку интервала не будет равным или больше х_max.

Для подсчета числа вариант, входящих в тот или иной интервал, удобно, просматривая последовательно статистические данные, проставлять черточки справа от соответствующего интервала. При этом в интервал включаются варианты больше левой границы и меньше или равные правой границе. Число вариант, попавших в один интервал, называется частотой интервала.

Пример 4. В результате измерения веса 25 кроликов различной породы были получены значения, представленные в таблице:

3,2	4,5	5,2	5,6	6,6
3,8	4,7	5,2	5,7	6,3
4,1	4,9	5,3	5,8	6,4
4,3	5,0	5,3	5,8	6,7
4,3	5,1	5,4	5,9	7,3

Из таблицы видно, что х_max = 7,3, x_min = 3,2. Определим величину интервала 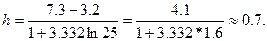Можно взять h=1. тогда левой границей первого интервала будет число x_min – h/2=3,2-0,5=2,7.

Таблица 4.

Распределение кроликов по весу

Интервалы	ni (частоты)
2.7-3.7
3.7-4.7
4.7-5.7
5.7-6.7
6.7-7.7

n = 25

Дата добавления: 2014-01-20