Виды случайных событий. Алгебра событий

Пусть производится опыт, который имеет ряд возможных событий (исходов): А, В, С и т. д.

1. События А, В, С,... называются единственно возможными, если в результате каждого испытания хотя бы одно из них наверное наступит.

Говорят также, что рассматриваемые события образуют пол­ную группу событий. Например, при бросании игрального кубика единственно возможные события, состоящие в выпадении одного, двух, трех, четырех, пяти и шести очков, образуют полную группу событий.

2. События называются несовместными, если в результате опыта появление одного ис­ключает появление остальных событий. Например, в ящике находится пять шаров, помеченных номерами: 1, 2, 3, 4, 5.
При извлечении шара вскроется только один из пяти номеров,
значит, события, состоящие в появлении этого номера при
дальнейшем извлечении шаров из ящика, являются несовме­стными.

3. События называются равновозможными, если при испытании не существует никаких объ­ективных причин, вследствие которых одно из них могло бы наступать чаще, чем другое. Например, появление герба или
решки при бросании монеты - события равновозможные. Но
если в ящике находится восемь белых и два черных шара,
то появления белого или черного шара не могут быть события­
ми равновозможными. Они носят название событий неравно-
возможных.

Единственно возможные, несовместные и равновозможные события называются случаями.

Случаи, способствующие появлению одного из неравновозможных событий, называются благоприятствующими этому событию.

4. Достоверные события. Событие называется достовер­ным, если оно в данном опыте непременно произойдет. Досто­верные события равносильны между собой, их можно обозначать одной буквой. Например, достоверное событие — появление белого шара из урны, содержащей только белые шары. 5. Невозможные события. Событие называется невозмож­ным, если оно заведомо не может произойти. Все невозможные
события равносильны между собой. Пример невозможного
события — извлечение красного шара из урны, содержащей
только белые и черные шары.

6. Противоположные события. Событие, состоящее в том,
что некоторое событие А не происходит, называется противо­положным событию А.Например, при подбра­сывании монеты для события А — выпадение герба — противо­положным является выпадение решки.

В теории вероятностей над событиями производят различные действия (сложение, умножение, вычитание), совокупность которых образует так называемую алгебру событий.

1. Суммой или объединением двух событий А и В называется такое событие С, которое состоит или в осуществлении события А, или события В, или событий А и В вместе.

Сумма событий обозначается как

С = А + В или С = А È В.

Суммой любого числа событий А₁, А₂, …, А_п называется событие С, которое состоит в осуществлении хотя бы одного из этих событий.Это записывается в виде

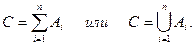
Следствие. Если события А₁, А₂, …, А_п несовместны, то их сумма А₁+А₂+ …+ А_п есть событие, состоящее в наступлении одного и только одного из этих событий.

Система несовместных событий А₁, А₂, …, А_п называется полной, когда известно, что при выполнении комплекса условий одно из событий этой системы должно с достоверностью произойти.Для полной системы несовместных событий

А₁+А₂+ …+ А_п = U.

Простейшей полной системой событий является система противоположных событий.

2. Разностью событий А и В называется событие С, состоящее в том, что в результате испытания произошло событие А и одновременно не произошло событие В.

Разность событий обозначается как

С = А – В.

3. Произведением или пересечением (совмещением) двух событий А и В называется событие С, которое состоит в осуществлении и события А и события В.

ВЕРОЯТНОСТИ СОБЫТИЯ. КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ СОБЫТИЯ.

Рассматривая множество событий, можно положить, что для каждого случайного события объективно существует специфическая мера возможности его появления в данном опыте, называемая вероятностью события. Это безразмерная величина, служащая в некотором смысле «мерой случайности» события, характеризующая степень его близости к достоверному событию. Поэтому вероятность достоверного события условились обозначать числом. Соответствующее соглашение является общепринятым и его называют постулатом.

Вероятность достоверного события U(W) равна 1, а вероятность невозможного события V(Æ) равна 0.

Вероятность любого события А обозначают символом Р(А), или Р_А, или р. Тогда

Р(U) = P(W) = 1; P(V) = P(Æ) = 0.

Классической вероятностью Р(А) события А называется отношение числа случаев т, благоприятствующих событию А, к общему числу случаев п:

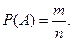(1)

Легко заметить, что для любого события А число благоприятствующих событий т удовлетворяет неравенству 0 £ т £ п, поэтому вероятность любого события А подчинена условию

0 £ Р(А) £ 1.

Пример 1. В урне находится 2 белых и 3 черных шара. Из нее наугад извлекается один шар. Найти вероятность того, что этот шар будет белым.

Решение. Обозначим через А событие, состоящее в появлении белого шара. Общее число случаев п = 5, число случаев, благоприятствующих событию А, т = 2, следовательно,

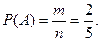
Формула (1) применялась для вычисления вероятностей событий с самого начала возникновения науки о случайных явлениях и долгое время рассматривалась как определение вероятности. В наше время формула (1) не является универсальной. Она пригодна только в тех опытах, которые обладают симметрией возможных исходов, то есть сводятся к схеме случаев. Кроме того, классическая вероятность определена лишь для конечного числа событий. В связи с запросами практики необходимо было ввести другие определения вероятности, которые могли бы в той или иной степени преодолеть эти недостатки.

Статистическая вероятность события. При рассмотрении классического и геометрического определений вероятности предполагалось, что случайные события равновозможны. Обычно о равновозможности случайных событий судят исходя из соображений симметрии. Например, при бросании игрального кубика предполагают, что он имеет форму правильного куба. Однако таких задач на практике встречается весьма мало. Поэтому в естественнонаучных и технических вопросах пользуются так называемым статистическим определением вероятности.

Допустим, что имеется возможность неограниченного повторения испытаний, в каждом из которых при сохранении неизменных условий отмечается появление или непоявление некоторого события А (бросание монеты, извлечение шара из урны, стрельба по цели).

Пусть при достаточно большом числе п испытаний интересующее нас событие А произошло т раз. Отношение

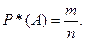(2)

называется относительной частотой события А в данной серии испытаний или просто частотой события А.

Частоту события иначе называют его статистической вероятностью.

Несмотря на внешнее сходство, формулы (1) и (2) различны по существу. Формула (1) служит для теоретического вычисления вероятности события по заданным условиям опыта. Формула (2) служит для экспериментального определения частоты события; чтобы ею воспользоваться, необходим опытный, статистический материал.

Между частотой события и его вероятностью существует некоторая связь: ясно, что более вероятные события происходят чаще, чем маловероятные. Если мы повторяем один и тот же опыт много раз (причем обеспечена независимость исходов отдельных опытов), частота события становится все менее и менее случайной, выравнивается и приближается к постоянной величине. Естественно предположить, что эта постоянная величина и есть не что иное, как вероятность события. Для опытов, сводящихся к схеме случаев, можно непосредственно убедиться, что эта постоянная равна вероятности события.

Дата добавления: 2014-01-20