Сочетания. Комбинаторика изучает способы подсчета числа элементов в различных множествах

Перестановка.

НАЧАЛЬНЫЕ СВЕДЕНИЯ ИЗ КОМБИНАТОРИКИ.

ПОВТОРНЫЕ ИСПЫТАНИЯ.

Комбинаторика изучает способы подсчета числа элементов в различных множествах. К этому подсчету сводятся многие практические и теоретические задачи. Комбинаторные методы применяются в теории вероятностей, статистике, экономике, физике, химии, биологии и других науках.

Рассмотрим наиболее употребительные формулы комбинаторики.

Пусть М – некоторое конечное множество, состоящее из п элементов:

М = {a, b, c, …, l}.

Перестановкой называется всякое расположение элементов данного конечного множества, получающееся при некотором упорядочении этого множества. Упорядочить множество – значит выбрать какой-либо элемент этого множества и назвать его первым, выбрать какой-либо другойэлемент и назвать его вторым и т. д., а последний элемент назвать п -м.

Число перестановок из п элементов равно произведению первых п натуральных чисел, то есть

Р_п = 1 × 2 × 3 × … × (п –1) = п!

Произведение п первых натуральных чисел обозначают через п! (читается: «эн факториал»).

При этом полагают 1! = 1 и 0! = 1. Из определения символа п! Вытекает следующее свойство:

п! = (п – 1)! п.

Например, 10! = 9! × 10 = 1 × 2 × 3 × 4 × 6 × 7 × 8 × 9 × 10.

Пусть множество М содержит п элементов. Число подмножеств множества М, состоящих из т элементов (безразлично в каком порядке выбираются элементы), называется сочетанием из п по т и обозначается символом .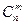

Для множества А { x, y, z }

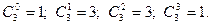
Основная формула для вычисления числа сочетаний из п элементов, взятых по т, 0 < m < n, имеет вид

Например,

.

Дата добавления: 2014-01-20