Лекция №3 Производящие функции

Рассмотрим рекуррентную последовательность { u_n } над полем Р, удовлетворяющую соотношению u_n+k + C ₁ u_{n+k -1} + … + C_ku_n = 0, n Î N. Первые k членов последовательности u ₁, u ₂, …, u_k будем считать фиксированными.

Определение. Функция вида A(x) = u ₁ + u ₂ x + u ₃ x ² + … + u_nx^{n -1} +…, называется производящей функцией рекуррентной последовательности { u_n }.

Пример. А(х) = 1+ x + 2 x ² + 3 х ³ + 5 х ⁴ + 8 х ⁶ +13 х ⁷+ … - производящая функция последовательности чисел Фибоначчи.

Определение. Формальным рядом назовем степенной ряд

u ₁ + u ₂ x + u ₃ x ² + … + u_nx^{n -1} +…,

где u_n - элементы поля Р.

Сумма формальных рядов A(x) =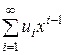и B(x)=определяется следующим образом: A(x) + B(x) = =.

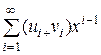Операция умножения формального ряда A(x) на скаляр l из поля Р определяется соотношением: l A(x) =lu ₁ + l u ₂ x + l u ₃ x ² + … + l u_nx^{n -1} +…

Введенные таким образом операции задают на множестве P _{[[ x ]]} формальных рядовструктуру бесконечномерного векторного пространства (P _{[[ x ]]}, P, +, *l).

Произведение формальных рядов является формальным рядом вида:

A(x)×B(x)==

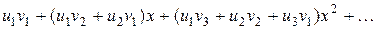
(P _{[[ x ]]}, +, ×) - ассоциативное коммутативное кольцо с единицей. Единичный ряд имеет следующий вид: 1 + 0× x + 0× x ² + … + 0× x^{n -1} +…, где 1 - единица поля Р.

Свойство. Формальный ряд A(x) =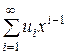обратим тогда и только тогда, когда u ₁ ¹ 0.

Рассмотрим способ получения производящей функции А(х) для рекуррентной последовательности u_n, удовлетворяющей соотношению:

u_n+k + C ₁ u_{n+k -1} + … + C_ku_n = 0.

Обозначим Р (х) = р ₁ + р ₂ х + р ₃ х ² + … + р_k х^{k -1} - многочлен, степень которого на единицу меньше порядка рекуррентности данного соотношения, его коэффициенты определяются из равенств:

р ₁ = u ₁,

р ₂= u ₂ + С ₁ u ₁,

р ₃ = u ₃ + С ₁ u ₂ + С ₂ u ₁,

…

р_k = u_k + С ₁ u_{k -1} + С ₂ u_{k -2} + … + С_{k -1} u ₁.

Многочлен F *(x) = 1 + С ₁ х + С ₂ х ² + … + С_kх^k получен из характеристического многочлена F (x) = х^k + С ₁ х^{k -1}+ С ₂ х^{k -2} + …+ С_k данного рекуррентного соотношения по правилу:

F *(х) = F (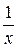) × х^k.

Производящая функция данной рекуррентной последовательности может быть получена по формуле:

А(х)=.

Пример. Найдите производящую функцию для последовательности чисел Фибоначчи.

Решение. Члены последовательности Фибоначчи удовлетворяют соотношению u_{n+ 2}- u_{n +1} - u_n = 0, u ₁ = u ₂ =1.

Составим характеристический многочлен F (x)= х ² - х -1. Двойственным для него будет многочлен F *(х) = ((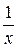)² - 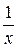-1) х ² = 1 - х - х ².

Коэффициенты многочлена Р (х) имеют вид:

р ₁ = u ₁ = 1, р ₂= u ₂ + С ₁ u ₁ = 1+(-1)×1=0.

Следовательно, Р (х) = 1. Получим производящую функцию А (х)= .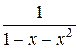

_ 1 1 - х - х ²

1 - х - х ² 1 + х + 2 х ² + 3 х ³ + …

_ х + х ²

х - х ² - х ³

_2 х ² + х ³

2 х ² - 2 х ³ -2 х ⁴

_3 х ³ + 2 х ⁴

3 х ³ - 3 х ⁴ -3 х ⁵

5 х ⁴ -3 х ⁵

…

А (х) = 1 + х + 2 х ² + 3 х ³ + …

Дата добавления: 2014-01-20