Вывод канонического уравнения эллипса

Эллипс

Решение.

Определение. Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух данных точек плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

Пусть F ₁ и F ₂ – фокусы, положим . Декартову систему координат зададим следующим образом: ось 0х направим по прямой F ₁ F ₂, а начало поместим в середину отрезка F ₁ F ₂. Тогда F ₁(- с,0), F ₂(с,0). (рисунок 2)

Рисунок 2

Пусть М (х, у) – произвольная точка эллипса. Тогдагде величина дана, причем .

Имеем:

, .

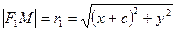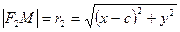И, следовательно, уравнение эллипса примет вид:

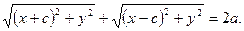
Упростим это уравнение: перенесем второе слагаемое в правую часть и возведем обе части в квадрат.

Получим,

после раскрытия скобок и приведения подобных получим:

Разделим полученное равенство на четыре и возведем обе части еще раз в квадрат:

преобразуем:

.

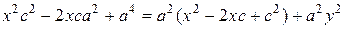После приведения подобных слагаемых получим:

Обозначим 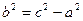и разделим обе части последнего равенства на эту величину:

(2) каноническое уравнение эллипса

где 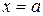и – полуоси и центром симметрии является точка (0, 0). Число в уравнении эллипса называется большой, а b - малой полуосью эллипса.

Прямую, на которой расположены фокусы эллипса, называют фокальной осью.

Величина 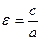называется эксцентриситетом эллипса, а прямые 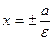называются директрисами эллипса.

Пример 2. Доказать, что уравнение 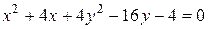определяет эллипс. Построить квп.

Дата добавления: 2014-01-20