Системы счисления. Система счисления (СС) – это совокупность приёмов и правил для записи чисел цифровыми знаками или символами

Система счисления (СС) – это совокупность приёмов и правил для записи чисел цифровыми знаками или символами.

Любая система счисления, предназначенная для практического применения, должна обеспечивать:

1) возможность представления любого числа в рассматриваемом диапазоне величин,

2) единственность представления, т.е. каждой комбинации символов должна соответствовать одна и только одна величина,

3) простоту оперирования числами.

Системы счисления делятся на:

1. непозиционные – это системы счисления, в которых значение символа не зависит от его положения в числе. Примеры: римская, палочковая, славянская, сирийская, египетская, вавилонская.

Способ представления непозиционной системы счисления в общем виде:

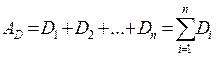
A_D – запись числа A в системе счисления D.

D_i – символы системы, образующие её базу.

2. позиционные – системы счисления, удовлетворяющая уравнению:

q – основание системы СС;

A_q – произвольное число, записанное в системе счисления с основанием q;

a_i – цифра (символ) системы счисления с основанием q;

n-1, m – количество целых и дробных разрядов в числе.

Сокращённый вариант: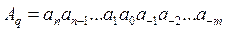

4	3	2	1	0	-1	-2	-3	-4	-5	-6	-7	=
				3,

=1*10⁴+2*10³+5*10²+7*10¹+3*10⁰+1*10^-1++3*10^-2+2*10^-4+8*10^-5+9*10^-6+1*10^-7.

Для естественной позиционной СС q – основание системы (положительное целое число).

В позиционной системе счисления значение цифры определяется её положением в числе: один и тот же знак принимает различные значения.

Любая позиционная система счисления характеризуется основанием. Основание (базис) q естественной позиционной системы счисления – это количество знаков или символов, используемых для изображения числа в данной системе. Возможно бесчисленное множество позиционных систем счисления, т.к. приняв за основание любое число, можно образовать новую систему счисления.

Диапазон представления чисел в заданной системе счисления – это интервал числовой оси, заключённый между максимальными и минимальными числами, представленный длиной разрядной сетки.

Дата добавления: 2014-01-20