Гидростатика

Лекция 6

Процессы и аппараты

Гидромеханические

Химической технологии

Типовые процессы и аппараты

II – часть

В гидростатике рассматриваются условия (законы) равновесия покоящейся жидкости. Поскольку жидкость находится в состоянии покоя, в ней не проявляются силы вязкого трения. В покоящейся жидкости действуют массовые и поверхностные силы.

В работе [1] из уравнения Навье – Стокса (как частный случай) было получено уравнение равновесия Эйлера:

(1.1)

Распишем это уравнение по осям в декартовой системе координат:

(1.2)

где X, Y, Z – проекции единичных массовых сил по осям x, y, z; , , – градиенты давлений по направлениям осей x, y, z.

Преобразуем систему уравнений (1.2). Для этого первое уравнение системы (1.2) умножим на dx, второе – на dy, третье – на dz и, сложив эти три уравнения, получим:

.

Правая часть полученного уравнения представляет собой полный дифференциал давления. Следовательно, можно записать:

. (1.3)

Полученное уравнение не содержит частных производных и более удобно для практического использования. Уравнение (1.3) называется основным дифференциальным уравнением гидростатики. Так как dp является полным дифференциалом, а плотность жидкости r является постоянной величиной, то выражение в скобках правой части будет также полным дифференциалом некоторой функции координат dU (x, y, z). Эта функция является потенциалом сил. Таким образом, равновесие жидкости возможно, если массовые силы имеют потенциал.

Уравнение (1.3) дает закон распределения давления внутри жидкости при заданной системе сил.

Рассмотрим поверхность равного давления. Для этого случая , поскольку 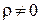, тогда в качестве общего уравнения поверхности равного давления в декартовой системе координат получим:

. (1.4)

Некоторые свойства поверхности равного давления:

– две поверхности уровня не пересекаются (для одной поверхности , для другой – , в точке их пересечения было бы , а это не так);

– внешние массовые силы направлены нормально к поверхности уровня (доказательство от обратного).

Свободная поверхность – поверхность, граничащая с газовой средой – является одной из поверхностей равного давления. Поверхность равного давления относительно Земли представляет собой семейство горизонтальных плоскостей:

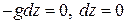, т.е. . (1.5)

В этом случае из массовых сил действует только сила тяжести.

Дата добавления: 2014-01-20