Сплайновая интерполяция

Полиномиальная сплайн-интерполяция

Полиномиальная аппроксимация

Экспоненциальная регрессия

Полиномиальная регрессия

Реализация полиномиальной регрессии

Интерполяция по общей формуле Лагранжа

Сплайновая интерполяция

Для задания векторов узловых точек VX и VY и заданного аргумента х функция linterp (VX,VY,x) возвращает значение функции при её линейной аппроксимации (интерполяции). При экстраполяции используются отрезки прямых, проведенных через две крайние точки.

При небольшом числе узловых точек (менее 10) линейная интерполяция оказывается довольно грубой. При ней даже первая производная функции аппроксимации испытывает резкие скачки в узловых точках. Для целей экстраполяции функция linterp не предназначена и за пределами области определения может вести себя непредсказуемо.

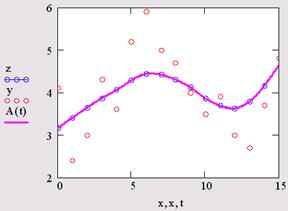
Гораздо лучшие результаты даёт сплайн-интерполяция. При ней исходная функция заменяется отрезками кубических полиномов, проходящих через три смежные узловые точки. Коэффициенты полиномов, проходящих через три смежные узловые точки. Коэффициенты полиномов рассчитываются так чтобы непрерывными были первая и вторая производные. Линия, которую описывает сплайн-функция, напоминает по форме гибкую линейку, закреплённую в узловых точках.

Для осуществления сплайновой интерполяции система Mathcad предлагает четыре встроенные функции. Три из них служат для получения векторов вторых производных сплайн функций при различных видах интерполяций:

cspline (VX,VY) – возвращает вектор VS вторых производных при приближении в опорных точках к кубическому полиному;

pscline (VX,VY) – возвращает вектор VS вторых производных при приближении в опорных точках к параболической кривой;

lspline (VX,VY) – возвращает вектор VS вторых производных при приближении в опорных точках к прямой.

interp (VS,VX,VY,x) – возвращает значение y(x) для заданных векторов VS,VX,VY и заданного значения х.

Таким образом, сплайн-интерполяция проводится в два этапа. На первом с помощью одной из трех вышеописанных функций отыскивается вектор производных функции y(x), заданной векторами VX и VY её значений (абсцисс ординат). Затем на втором этапе для каждой искомой точки вычисляется y(x) с помощью функции interp.

Дата добавления: 2014-01-20