Обработка результатов эксперимента

Матрица планирования

Матрица планирования - зна­чения факторов приводятся в кодированном виде, зна­чения отклика — в реальном масштабе.

Матрица планирования имеет ряд свойств, наиболее важными из которых для нас являются следующие три:

a) симметричность — сумма всех элементов столбца каждого фактора равна нулю;

б) нормированность — сумма квадратов всех элемен­тов каждого столбца не зависит от рассматриваемого фактора и равна N;

в) ортогональность - сумма произведений соответ­ствующих элементов двух столбцов разных факторов равна нулю.

Одной из важнейших характеристик случай­ной величины является дисперсия, которая показывает степень ее сосредоточенности относительно среднего значения. В нашем случае дисперсия позволяет оце­нить уровень погрешностей в измерениях.

Дисперсией называется среднее значение квадрата отклонений величины от ее среднего значе­ния:

где - среднее арифметическое значение параметров оптимизации в некоторой точке плана, 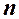- число параллельных опытов; - число степеней свободы f, равное в этом случае количеству опытов минус единица. При дублировании опытов для вычисления среднего использована одна степень свободы равная единице.

При расчете среднего значения суммируют все измерения и делят на их число. При этом надо исключить резко отличающиеся результаты, так называемые выбросы, например, воспользовавшись критерием Стьюдента t(p, f), где p - уровень значимости.В качест­ве р выбирается такое число, чтобы событие с этой вероят­ностью считалось практически невозможным; обычно полагают р = 0.05:

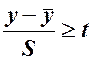
Значение 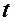берут из таблицы t(p, f) - распределения Стьюдента. Опыт считается вы­бросом, если экспериментальное значение критерия 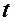при обычно ис­пользуемом уровне значимости 0.05 по модулю больше табличного. Такой расчет справедлив, если распределение всех результатов измерения является нормальным.

После того как реализованы опыты во всех точках плана и определены их дисперсии, следует убедиться в однородности дисперсий. Это является одним из требований регрессионного анализа, применение которого при исследовании свойств получаемых моделей возможно только при соблюдении всех его предпосылок.

Проверка однородности дисперсий проводится по различным критериям. Если число дисперсий больше двух, одна из них значительно превышает остальные и выполняется условие равного числа опытов во всех точках плана, то используется критерий Кохрена G(p,f₁,f₂), во всех других используют критерий Фишера.

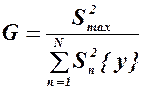
Число степеней свободы для числителя f₁=n_max-1, для знаменателя - f₂=N, где N число опытов.

Дисперсии однородны, если

Если используют критерий Фишера F(p, f₁, f₂), то

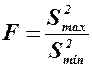
Если при числе степеней свободы числителя , а знаме­нателя 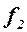для уровня значимости 0.05 , то дисперсии однородны.

Убедившись в однородности дисперсий, определяем диcпepсию параметра оптимизации по всем проведенным экспериментам или дисперсию воспроизводимости эксперимента:

Эта дисперсия показывает, насколько хорошо воспроизводятся (повторяются) значения отклика в случае постановки нескольких опытов при неизменных значениях факторов, то есть она характеризует величину помех (погрешностей) в эксперименте, иначе, точность эксперимента.

Реализовав эксперимент и вычислив средние значения откликов для каждой точки плана, необхо­димо проверить значимо ли отличаются друг от друга максимальное и минимальное 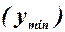из полученных значений по всему плану. Значимость различия двух средних можно проверить также с помощью t(p, f) - критерия (Стьюдента) по формуле:

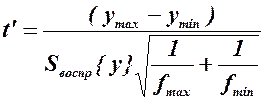
Средние значимо отличаются друг от друга, если экспериментальное значение критерия пре­восходит табличное для числа степеней свободы равной сумме f каждого опыта икритерия значимости 0.05.

Если же статически разница между и не значима, то значения параметра оптимизации во всех точках ПФЭ совпадают в пределах ошибки воспроизводимости экcпepимeнтa и дальнейшая обработка, результатов не имеет смысла. В этом случае необходимо расширять интервалы варьирования факторов или уменьшать дисперсию.

Дата добавления: 2014-01-20