Получение регрессионной зависимости методом наименьших квадратов (МНК)

В результате, проведения ПФЭ получена система линейных уравнений вида (1), коэффициенты b₀, b₁,… b_k которой необходимо определить. Для этого может быть применен простой и эффективный способ получения оце­нок коэффициентов регрессии - МНК. Со­гласно этому методу, коэффициенты должны выби­раться так, чтобы минимизировать сумму квадратов разностей между измеренными значениями перемен­ной у_i в каждой точке и теми ее значениями, которые предсказаны с помощью модели (1) –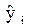. Если обозначить сумму как U. то

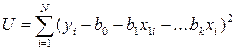
Согласно методу наименьших квадратов находятся такие значения оценок b₀, b₁,… b_k, которые мини­мизируют сумму квадратов отклонений U опытных точек от величин, предсказанных регрессион­ным уравнением.

В планировании эксперимента используется стандартная техника решения таких задач (взятие производных по b₀, b_1,….b_k, составление системы уравнений и ее решение). Рассмотрим эту процедуру для одного фактора:

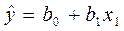
Необходимо вычислить 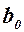и . Если бы экспериментальные точки строго лежали на линии 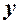, то

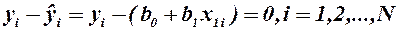
На практике возникает отклонение экспериментальных точек от теоретической линии - невязка.

Согласно методу наименьших квадратов находятся такие значения оценок 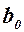,, которые мини­мизируют сумму квадратов отклонений (невязок) опытных точек от величин, предсказанных регрессион­ным уравнением:

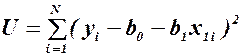
Известно, что минимум, если он существует, достигается при одновременном равенстве нулю частных производных по всем коэффициентам:

.

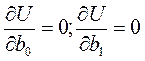
Тогда указанная процедура в МНК делает определенной любую систему уравнений, то есть число урав­нений становится равным числу неизвестных.

Отсюда находим 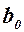и .

Дата добавления: 2014-01-20