Лекция №3. Дифференциальные уравнения с разделяющимися переменными и приводящиеся к ним

Дифференциальные уравнения с разделяющимися переменными и приводящиеся к ним.

Определение 12. Дифференциальные уравнения вида:

или

Делим обе части на:

– переменные разделились.

Пример 8. Проинтегрировать дифференциальное уравнение:

(3.9)

Разделим обе его части на 𝑥² и получим:

Откуда:

или

(3.12)

Уравнение (3.12) называется однородным, соответствующим дифференциальному уравнению (3.11).

Уравнение (3.12) - с разделяющимися переменными, проинтегрируем его:

При делении на 𝑦 теряем решение равнения (3.12) 𝑦 ≡ 0, решение (3.12) имеет вид:

(3.13)

С - произвольное действительное число.

(при С=0 формула (3.13) даёт и потерянное речение 𝑦≡0).

Для нахождения решения (3.11) применим так называемый метод вариации произвольной постоянной, который заключается в следующем. Решение (3.11) ищем в виде, аналогичном (3.13):

(3.14)

считая С(x) некоторой неизвестной функцией от x.

Подставим (3.14) в (3.11) и получим:

Отсюда:

(3.15)

Интегрируем (3.15) и находим:

тогда

Пример 9. Проинтегрировать уравнение:

и далее

(3.17)

или

Интегрируем обе части:

(3.18)

Для (3.17) 𝑦≡0 - потерянное решение ⟹ все решения (3.17) даются формулой, где C - любое действительное число. (при С=0 и потерянное решение 𝑦 ≡ 0 входит в (3.18).

Решение (*) ищем в виде:

(3.19)

Подставляем (3.19) в (*):

и.

Тогда

2.5. Теорема существования и единственности решения задачи Коши для дифференциального уравнения

Дифференциальных уравнений, интегралы которых находятся в результате конечной последовательности элементарных действий и дальнейшего интегрирования, немного. (Уже уравнение Риккати ставится следящим обрезом.

Требуется нейти решение дифференциального уравнения:

(5.1)

удовлетворяющее начальному условию:

(5.2)

Теорема 1. (о существовании и единственности решения задачи Коши) Пусть в уравнении (5.1)

1) функция непрерывна в области G: x₀–a ≤ x ≤ x₀+a; 𝑦₀–b ≤ 𝑦 ≤ 𝑦₀+b;

2) функция удовлетворяет условию Липшица по переменной 𝑦:

.

Тогда существует и притом единственное в промежутке решение уравнения (5.1), удовлетворяющее начальному условию (5.2),

Замечание 1 (к условию Теор.1). Интегральная линия, удовлетворяющая условию (т.е. проходящая через точку может выйти за пределы области G (Рис. 4),

x₀

x₀+a

x₀–a

y₀

y₀+b

y₀–b

(x₀, y₀)

Рис. 4

поэтому мы утверждаем существование решения в более узком промежутке.

Замечание 2. Условие Липшица можно заменить более "грубым", но легче проверяемым условием ограниченности в области G.

В самом деле, пусть, и пусть, тогда по теореме Лагранжа

Содержание

4 Динамический анализ механизмов и машин

4.1 Задачи динамического анализа

4.2 Силы, действующие в механизме

4.3 Силовой расчет механизмов (1-ая задача динамического анализа)

4.3.1 Построение кинематической схемы

4.3.2 Структурный анализ механизма

4.3.3 Построение плана скоростей и ускорений

4.3.4 Добавляем силы инерции F_H и моменты сил инерций звеньев Т_Н

4.3.5 Определяем реакций связей, уравновешивающий момент

Лекция №3

4.1 Динамический анализ механизмов и машин

Динамический анализ механизмов - это

- изучение методов определения сил, действующих на тела, образующая механизм, во время увеличения этих тел;

- изучение взаимосвязи между движениями этих тел, силами, на них действующими, и массами, которыми обладают эти тела. (стр. 19)

Динамический анализ механизмов имеет цели:

- силовой анализ механизмов: изучение влияния внешних сил, сил веса звеньев, сил трения сил инерций (массовых сил) на звенья, КП и неподвижные опоры; установление способов уменьшения динамических нагрузок;

- динамика механизмов: изучения режима движения механизма под действием заданных сил и установление способов, обеспечивающих заданные режимы движения механизмов.

Задачи динамического анализа:

1) Определение сил, действующих на элементы механизмов;

2) Составление уравнения движения машины;

3) Установление истинного закона движения машины под действием заданных сил;

4) Регулирование хода машины;

5) Уравновешивание масс в машине;

6) Изучение колебательных процессов в машине и способов виброгашения.

Силовой расчет механизма – определение силы трения и реакции связей в КП, силы инерций звеньев и др. силы, возникающие при движении механизма, если известные внешние силы, действующие на звенья механизма и законы движения звеньев.

Статический расчет – определение сил в механизме без учета дополненных сил, сил инерций звеньев возникающих при движении механизма; производился до появления в технике быстроходных машин.

Динамический расчет – определение сил в механизмах с учётом как статических так и динамических нагрузок, возникающих при движении механизма и часто превышающих статические силы.

В ТММ широкое применение получил метод силового расчета механизмов на основе уравнений равновесия твёрдых тел в форме Даламбера – метод обращения ускоренного или замедленного движения звеньев механизма в равномерное путём добавления к внешним силам фиктивных сил инерции.

Кинетостатический расчет механизмов - метод силового расчета механизма с использованием сил инерции и применением уравнений динамического равновесия.

Принцип Даламбера

Основной закон классической механики (один из основных законов): всякой силе действия есть равная, но противоположная сила противодействия, (ТММ, стр.9)

Аксиома связей: всякую связь можно отбросить и заменить силой, реакцией связей (в общем случае).

Активные силы – силы кроме сил реакций связей (ТММ, стр. 348)

Первоначально законы Ньютона, применяемые для рассмотрения движения свободной материальной точки, свободного твердого тела.

Для рассмотрения движения несвободных систем Даламбер, предложил специальный принцип, получивший название принципа Даламбера: при движений материальной точки активные силы, реакции связей вместе с силой инерции точки образуют равновесную систему сил, т.е.: уравнения движения несвободной материальной точки являются такими же как и для свободной, только к действующим на точку активным или заданным силами добавляют силы реакций связей.

Уравнение движения материальной точки m*ā=F+R, где

m – масса точки

а – ускорение точки относительно инерционной системы отчета (стр. 272)

F - равнодействующая активных сил;

R – равнодействующая реакций связей.

Назовем силой инерции точки произведение массы точки на вектор ускорения, взятое с обратным знаком, т.е.

Ф=-m*a, где

Ф – сила инерции.

Перенесем слагаемые в правую часть:

Точка движения с ускорением а под действием тел с силой равной (F+R).

По закону о равенстве сил действия и противодействия оказывать противодействие этим телам силой – (F+R), т.е. Ф=-(F+R). Это соотношение позволяет считать, что сила инерции приложена к «ускоряющим» телам. Эту силу переносим на материальный объект – точку, действующую силой инерции Ф на «ускоряющие» тела.

Переносная (релятивная) и кориолисова силы инерции являются частью полной силы инерции Ф. Если для части силы невозможно указать теля, которые ее создают, то это справедливо и для всей силы инерции Ф. Однако в рассматриваемом случае есть материальный объект, который действует с силой инерции Ф на ускоряющие тела.

Направления сил инерции противоположны направлениям ускорений рассматриваемых точек.

4.2 Силы, действующие в механизме

При работе механизма к его звеньям приложены внешние задаваемые силы: силы движущие; силы производственных сопротивлений; силы тяжести; моменты инерций, силы трения.

Движущие силы – те приложенные к звеньям силы, которые совершают положительную работу; другими: словами: те силы, которые стремятся ускорить движение механизма (работа этих сил - затрачиваемая работа).

Силы сопротивления – приложенные к звеньям силы, которые совершают отрицательную работу; другими словами те силы, которые стремятся замедлить движение механизма.

Силы полезного (производственного) сопротивления – те силы сопротивления, преодоление которых необходимо для выполнения требуемого технологического процесса (Совершаемая работа – полезная работа).

Силы вредных (непроизводственных) сопротивлений – те силы сопротивления, на преодоление которых затрачивается дополнительная работа (вредная работа) сверх той, которая необходима для преодоления полезного сопротивления.

Иногда называют: работу движущих сил – затрачиваемой работой;

Работу сил производственных сопротивлений полезной работой;

Работу сил непроизводственных сопротивлений вредной работой.

Примечание [ТММ, стр.247]

Условие статической определенности КЦ.

Статический расчет – в число заданных сил не входят силы инерции.

Кинетостатический расчет – в число заданных сил входят и силы инерции звеньев.

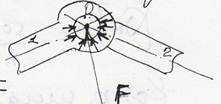Рассмотрим реакции в КП плоских механизмов.

Вращательная пара V класса.

Результирующая сила реакции F проходит через центр шарнира, Величина и направление этой реакции неизвестны, т.к. они зависят от величины и направления заданных сил, 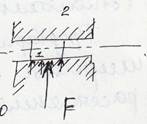приложенных к звеньям пары.

Поступательная пара V класса.

Реакция ┴ - а к оси движения х-х этой пары. Она известна по направлению, но неизвестны её точка приложения величина.

Высшая пара IV класса

Реакция F приложена в точке С касания звеньев 1 и 2 и направлена по общей нормами n-n, проведённой к соприкасающимся профилям звеньев 1 и 2 в т.с. Известны направление и точка приложения. Не известна величина.

Для определения реакций в каждой КП V класса необходимо найти по две неизвестных, в IV классе – одну неизвестную.

Для каждого звена, имеющего плоскопараллельное движение можно написать, три уравнения равновесия, то число уравнений для n подвижных звеньев з.п.

Число неизвестных, которое необходимо определить, будет равно для пар V класса 2*P₅, для пар IV класса 1*P₄.

Следовательно, КЦ будет статически определима, если удовлетворяется условие

3n=2*P₅+P₄.

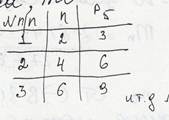Т.к. любой механизм с парами V IV классов может быть заменой КП V класса, то

3n=2P₅

P₅=3/2*n

(см.ТММ. стр.57) Это условие нам знакомо по рассмотренным группам различного вида, которые разбиты на классы.

Сила инерций F_и=-m*a_s, где

m – масса звена, кг.

a_s – вектор полного ускорения центра масс G_i звена.

Момент сил инерции M_n=-Y_s*E, где

E – условие ускорения, рад/с².

Y_s – момент инерции звена относительно оси, проходящей через центр масс J и ┴ - ый к плоскости движения звена кг*м².

4.3 Силовой расчет механизмов (1ая задача динамического анализа)

Примечание:

1) При силовом расчете необходимо пометить, что число неизвестных внешних сил в КЦ не должно превышать числа степеней свободы W этой цепи.

2) Так как группа Ассура имеет W=0, к её звеньям не могут быть приложены неизвестные внешние силы.

Определение реакций в кинематических парах механизма и уравновешивающего момента по методу Бруевича Н.Г.

(кинетостатический метод планов сил)

Силовой расчет проводят для определенного положения механизма, например первого.

Построение кинематической схемы.

4.3.1. Изображаем в определенном масштабе кинематическую схему заданного механизма.

K_L=QA/OA,M/MM [6’,6”]

Дано: W₁=const; E₁=0

Длины звеньев ОА, АВ

Массы звеньев m₁;m₂;m₃;

Моменты инерции звеньев Y₁₁;Y₁₂;Y₁₃

Сила полезного сопротивления F_n*c

Или момент полезного сопротивления (направляются против движения звена, к которому приложены);

Силы вредного сопротивления (силы трения) F_b*c=C

Определить: R₁₄; R₁₂; R₂₃; R₃₄; - реакции звеньев

T_ур – уравновешивающий момент

4.3.2 проводим структурный анализ механизма

W=3n-2P₅=3*3-2*4=9-8=1

За начальное звено принимают то, к которому приложена определяемая внешняя уравновешивающая сила F_ур или момент Т_ур.

4-1 + 2-3

HM + гр. Ассура II вид II кл механизм II класса

4.3.3Строим планы скоростей и ускорений

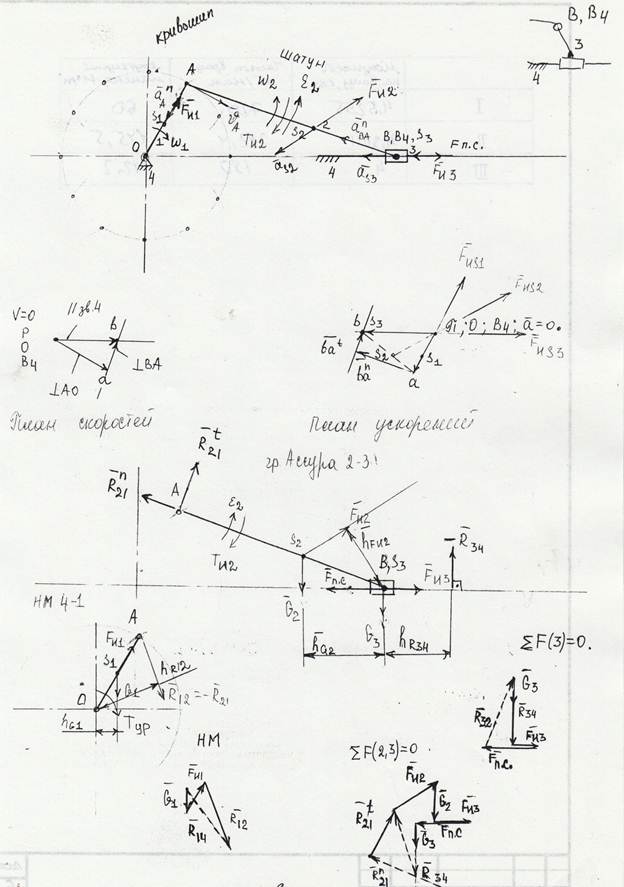
Из плана скоростей определяем неизвестные скорости

V_ВА=(ва)K_V

V_ВА=W₂BA; W₂=V_ВА/ВА=(ва)K_V/ВА*K_L

Для определения направления вращения звена 2 мысленно прикладываем V_ВА к точке В

Из плана ускорений определяем неизвестные ускорения

А^t_ba= (ba^t)K_a

А^t_ba= E₂BA; E₂= А^t_ba/BA=(ba^t)K_a/BA*K_L

Определяем направление: мысленно переносим вектор и прикладываем к точке В

A_B=(Пв)к_а

4.3.4 Добавляем силы инерции F_n и моменты сил инерции звеньев Т_и

Это выполняется для того, чтобы нейтрализовать ускорения и применить для решения уравнения статики.

↑F_HSi=m_i↓a_si Вектор силы инерции направляют с сторону, противоположную вектору ускорения

↓T_HSi = J_si↑E_i Вектор момента сил инерции направляют в сторону, противопложную угловому ускорению

J_si – момент инерции звеньев

А) Кривошип

Б) Шатун

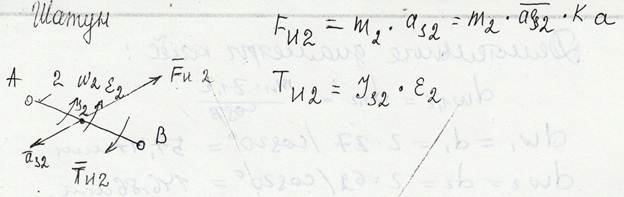
В) Ползун

Г) Коромысло (в нашем механизме отсутствует)

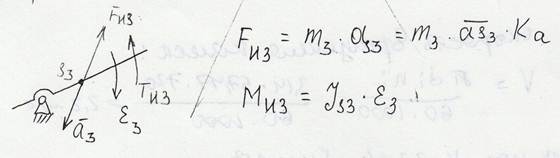
4.3.5 Определяем реакции связей и уравновешивающий момент

Определение реакции связей начинаем с последней присоединенной группы Ассура, заканчиваем начальным механизмом.

А) Группа Ассура 2-3 ® II класс, 2 вид, K_L=AB/AB, М/ММ

Последовательность определения реакций:

1) SТ_В(2)=0 ® R^t₂₁; решение аналитическое,

2) SF(2,3)=0 ® Rⁿ₂₁,R₃₄; решение графическое из плана сил

3) SТ_В(3)=0 ® h_R34; решение аналитическое,

4) SF(3)=0 ® R₃₂; решение графическое их плана сил

R₃₄-реакци связи на третье звено со стороны четвертого

R₂₁- реакция связи на второе звено со стороны перового

Примечание:

А) неизвестные параметры лучше располагать в начале и конце уравнения;

Б) не отрывать нормальную составляющую от тангенциальной;

В) лучше группировать силы для одного звена, а затем для другого.

1)

2)

3)

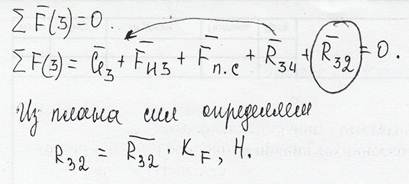
4)

Б) Начальный механизм

Последовательность определения реакций:

1) ; решение графическое

2) ; решение аналитическое

1)

Из плана сил:

2)

Уравнение кинетостатики для других видов групп Ассура представлены в раздаточном материале.

Чтобы имело место равновесие в Н.М. необходимо дополнительно ввести силу или пару сил, уравновешивающие все силы, приложенные к начальному звену, Эта сила и момент носят название уравновешивающей силы и уравновешивающего момента.

Таким образом, уравновешивающим моментом называют момент сил, действующих на начальное звено, обеспечивающий заданный закон его движения М_ур.

Аналогично определяется уравновешивающая сила F_y.

1* Скорость (Высш.мат.стр.154)

Определение: Если точка движется по прямой (для простоты рассуждений), то средней скоростью её за некоторый промежуток времени называется отношение пути, пройденного за этот промежуток времени к его длительности.

V_ср=S/T, где Т – продолжительность промежутка времени; S – путь пройденный за этот промежуток времени.

Определение: Истинной скоростью точки в данный момент называется предел средней скорости этой точки за бесконечно малый промежуток времени, стягивающийся в данный момент

2* Определение производной.

Пусть y=f(x) – некоторая функция.

Проделаем следующие 5 операций:

1. Придадим аргументу некоторое постоянное значение Х и вычислим y=f(x).

2. Придадим аргументу приращение Dх₁, последующее новое значение x+Dx и вычислим y+Dy=f(x+Dx).

3. Вычислим приращение функции Dy=f(x+Dx)-f(x)

4. Составим соотношение

5. Устремим DХ к нулю и будем искать предел

Этот предел называется производной функции f(x) в точке х и обозначается так:

y’; y_x’; f’(x); (f(x))’.

Определение: производная есть предел отношения приращения функции к вызвавшему его бесконечно малому приращению аргумента.

y’=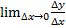

Действие нахождения производной какой-нибудь функции называется дифференцированием этой функции.

Первообразная.

Основной задачей дифференцирования является нахождение скорости изменения какой-нибудь функции.

Обратная задача: зная скорость изменения функции, найти эту функцию

Эта операция называется интегрированием этой функции.

Определение: функция F(x) называется первообразной для функции F(x), если эта последняя является производной от F(x). f(x)=F’(x)

Например F’(x)=3x²; F(x)=x³ - первообразная

y=x³, но мы имеем первообразную Z=x³+5, т.к. (x³+5)’=3x²

В таком виде первообразная F(x)+C – представляет общий вид или полное семейство первообразных для f(x)

Определение: Если F(x) есть какая-то первообразна для F(x), то выражение F(x)+C, где С может принимать любое постоянное значение, называется неопределенным интегралом функции ф(х) и обозначается через ∫f(x)dx.

∫f(x)dx=F(x)+C, где С – произвольная постоянная

f(х) - подынтегральная функция

4* Определенный интеграл

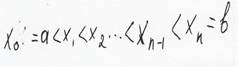Геометрический смысл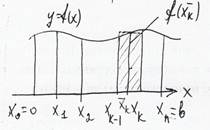

Найдем площадь F этой кривой

- сумма Римана

, где λ – ранг дробления

Если устремить к 0 ранг дробления, то сумма Римана будет стремится к некоторому пределу, который называется определенным интегралом от функции ф(х) по промежутку (а,в) и обозначается символом

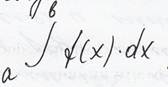
Определение: Определенный интеграл есть конечный предел суммы Римана при стремлении к нулю ранга дробления, порождающего эту сумму

5*Фундаментальная формула Ньютона-Лейбница.

Правило. Для вычисления определенного интеграла от какой-нибудь функции надо найти для неё первообразную и составить разность значений этой первообразной при верхнем и нижнем пределах интегрирования (стр. 268)

6* Таблица основных интегралов

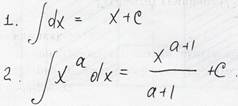
7* Механическое применения определенного интеграла.

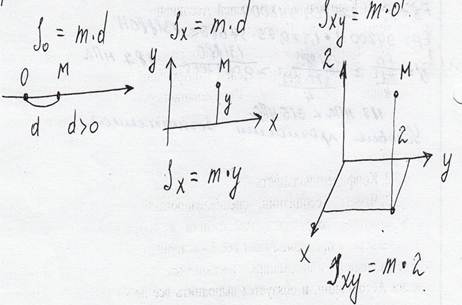
Момент инерции материальной точки М относительно точки О (или прямой ОХ, или плоскости ХУ) называется произведение массы м точки М на квадрат её расстояния d от точки О (или соответственно от прямой ОХ, или плоскости ХУ) т.е.

Статическим моментом So (Sx Sxy) точки М относительно О (или Ох, или ху) называется произведение массы m точки М на первую степень расстояния d:

8* Моменты плоских фигур

Прямоугольники

Масса равномерно распределена по той или иной плоскости фигуры, причем плотность ровна единице.

Масса плоскости ровна её площади а*d2,а расстояние от всех её точек до основания равна 2

Круг. Момент инерции Jo круга радиуса R относительно его центра О

Площадь кольца, следовательно, масса элементарного кольца, равна 2π*r*dr, все его точки удалены от центра на расстояние r тогда –

Дата добавления: 2014-01-20