Л4. Сферические треугольники и их типы

При решении задач судовождения Землю принимают за сферу. Сферой называют поверхность, все точки которой равноудалены от одной точки, называемой центром сферы.

Радиусом сферы является отрезок прямой, который соединяет центр сферы с любой её точкой.

Всякое сечение сферы плоскостью называется окружностью или кругом. Большим кругом является любое сечение сферы, проходящее через её центр. Этот круг больше любого другого сечения, которое не проходит через центр сферы и называется малым кругом.

Радиус большого круга равен радиусу сферы (ОВ на рис.6). Ось круга (POP´) – это перпендикуляр из центра круга O или O´ к его плоскости.

Полюса круга – это точки пересечения оси круга с поверхностью сферы в диаметрально противоположных направлениях (точки P и P´).

Cферическим радиусом большого круга (например, ABC) является дуга другого большого круга (ДБК) между его любой точкой и полюсом (ДБК: PA´A или PB´B, или PC´C). На рис. 6 малый круг А´В´С´ и его сферический радиус – ДБК или PA´, или PC´. Точки P и P´ являются полюсами большого и малого кругов.

ДБК называется ортодромией и является кратчайшим расстоянием между двумя точками на сфере, подобно тому, как прямая линия является кратчайшим расстоянием между точками на плоскости. Этим объясняется та большая роль, которую играют ортодромии при решении многих задач судовождения, и в этом заключается основное свойство ДБК: меньшая из ДБК, проходящих через две заданные точки сферы A и B (дуга ADB), является кратчайшим расстоянием между этими точками (через точки A и B проходит и ДБК ACB).

Cферическим треугольником (СфТ) называется фигура на сфере, образованная тремя пересекающимися попарно ДБК, которые не пересекаются в одной точке. На рис. 6 сферическим треугольником является фигура APB, а A´P´B´ – нет. Отсюда следует, что сферический треугольник APB образован тремя ДБК, которые являются ортодромиями между точками A и P, P и B, B и A.

Сферическими треугольниками будут и фигуры AP´B, BP´C, BPC.

Рассмотрим сферический треугольник ABC на рис. 7, который образован ДБК, проходящими через точки A и B, А и С, В и С. Принято обозначать углы сферического треугольника большими (прописными) буквами латинского алфавита, а противолежащие им стороны – соответствующими им малыми (строчными) буквами.

Стороны сферического треугольника, являясь ДБК (ортодромиями), измеряются в дуговой мере, т.к. они не зависят от радиуса сферы и численно равны плоским углам при центре сферы, образованным соответствующими радиусами сферы.

Например, сторона a измеряется углом СОВ, сторона b – углом АОС, c – АОВ. Следовательно, сумма сторон сферического треугольника всегда больше нуля, но меньше 360º.

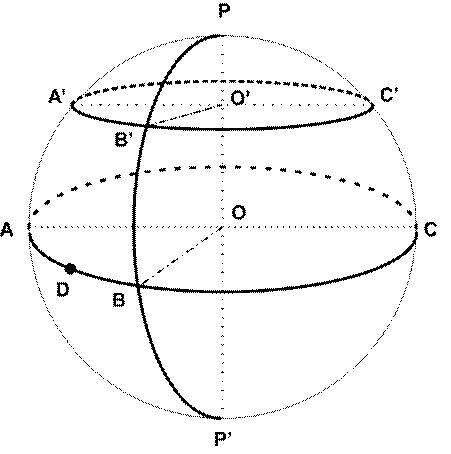
Рис. 6. Основные линии и точки на сфере

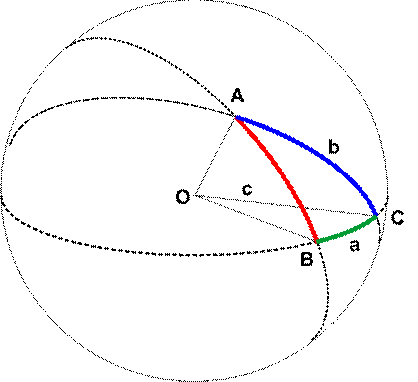
Рис. 7. Сферический треугольник

Если сумма сторон треугольника равна 360º, то это означает, что такая фигура является полусферой.

Итак, 0º<a+b+c<360º. Для сферического треугольника справедливы следующие неравенства:

a+b>c; b>a-c; a<(a+b+c)/2.

Углы A, B, C сферического треугольника также измеряются в дуговой мере (градусы, минуты, секунды). Они численно равны соответствующим двугранным углам трёхгранника ОАВС и по свойству этих углов сумма углов сферического треугольника всегда находится в пределах

180º<A+B+C<540º.

Это свойство углов сферического треугольника записывают так: A+B+C=180º+ε.

Величину ε называют сферическим избытком или эксцессом.

При ε=0 СфТ превращается в плоский, при ε=360º СфТ – в полусферу.

Углы и стороны СфТ называют его элементами. Эти элементы связаны между собой следующими соотношениями:

– против равных сторон лежат равные углы, а против б о льших сторон лежат б о льшие углы;

– сумма двух углов без третьего всегда меньше 180º, т.е.

A+B-C<180º; B+C-A<180º; A+C-B<180º.

В навигации и мореходной астрономии (см. рис.1) используются сферические треугольники, которые помещаются на одной половине сферы. Эти треугольники называют треугольниками Эйлера.

По форме сферические треугольники разделяют на косоугольные, прямоугольные и четвертные или прямосторонние. В прямоугольном треугольнике один из углов равен 90º. Но есть сферические треугольники с двумя и тремя прямыми углами, которые называют двояко- и троякопрямоугольными. По аналогии в прямостороннем треугольнике одна из сторон равна 90º и существуют двояко- и троякопрямосторонние треугольники. И, наконец, бывают сферические треугольники, у которых и углы, и стороны все равны 90º. Например, таким треугольником является ¼ сферы.

Дата добавления: 2014-01-20