Решение. При изменении действительного значения действующего значения напряжения цепи вольтметрам, имеющим заметную случайную погрешность получен ряд

Пример

При изменении действительного значения действующего значения напряжения цепи вольтметрам, имеющим заметную случайную погрешность получен ряд наблюдений(результатов одиночных прямых измерений).

N п/п

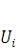
1. Определим оценку истинного значения результата измерения

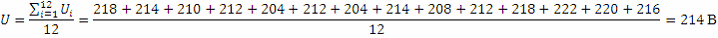
2. Определяем оценку среднего квадратичного отклонения

3. Определяем абсолютную погрешность многократного прямого измерения при доверительной вероятности

,

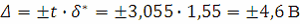Где t – коэффициент Стьюдента; при

4. Следовательно, результат многократных прямых измерений напряжения можно представить в виде:

Или

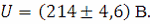
УЭ 1.4-4 Обработка косвенных измерений

Косвенные измерения в практике электрических измерений встречаются довольно часто. Вопрос оценки погрешности резуль­тата измерения — один из важнейших в таких экспериментах. Имея подробную исходную информацию о применяемых средствах из­мерения, измеряемых величинах и условиях проведения экспери­мента, можно достаточно строго решить задачу оценки суммарной погрешности результата измерения. Правда, требуется четко ого­варивать все допущения. Возможны два подхода к решению этой задачи: детерминированный и вероятностный, рассмотрим пер­вый подход.

Детерминированный подход (иногда называемый методом наи­худшего случая) более характерен для обычных технических изме­рений и экспресс-измерений с их обычно упрощенными моделя­ми процессов и подходами. Перед рассмотрением этого подхода оговорим необходимые допущения:

а) инструменты исправны, имеют реальные погрешности, соответствующие своим классам точности. Причем их погрешности — только систематические, т.е. не меняющиеся в течение данного эксперимента. Случайных погрешностей нет;

б) исходные измеряемые величины характеризуются неизменными (в течение данного эксперимента) значениями основных параметров;

в) условия работы СИ — нормальные или рабочие;

г) функциональная зависимость искомой величины Y от ис­ходных величин Xi известна достаточно точно;

д) оператор имеет достаточную квалификацию.

Если интересующая нас величина /связана с исходными вели­чинами Xj известной функциональной зависимостью F:

и предельные значения абсолютных погрешностей А,- определения каждой исходной величины Х_{ известны, то предельное значение абсолютной погрешности Д_г результата измерения искомой вели­чины У в общем случае можно определить по так называемой фор­муле накопления частных погрешностей:

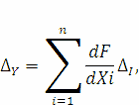
где 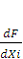- частные производные функционала F no каждой исходной величине в точках, соответствующих найденным значениям величин Xi,

∆_i- — предельные значения абсолютных погрешностей определения исходных величин Xj.

Рассмотрим два частных, но довольно распространенных, слу­чая функциональной зависимости F.

Первый частный случай — функционал F имеет вид суммы. Если функциональная зависимость имеет вид

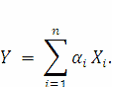
где о, — коэффициенты функциональной зависимости, то пре­дельное значение абсолютной погрешности ∆_Y определяется по формуле

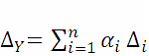
Относительная погрешность δ_У, %, при этом может быть най­дена обычным образом:

Например, если Y= 5Х₁ + 2Х₂ + Х₃, то ∆_Y= 5∆₁ + 2∆₂ + ∆з.

Второй частный случай — функционал F имеет вид произведе­ния. Если функциональная зависимость имеет вид

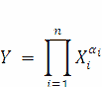
где П — знак произведения я сомножителей; α_i— коэффициенты — показатели степени исходных величин X_h то предельное значение относительной погрешности δ_Y определяется по формуле

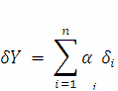
где δ_i,- — предельные значения относительных погрешностей опре­деления исходных величин X_t.

Предельное значение абсолютной погрешности A _Y затем нахо­дится обычным образом

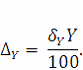
Например, если функционал У имеет вид

,

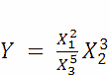то значение относительной погрешности

.

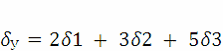И хотя формально третье слагаемое должно входить в сумму со знаком минус, но, поскольку предельные значения отдельных погрешностей практически всегда симметричны (±), то в худшем случае (самое неблагоприятное сочетание значений и знаков всех составляющих) предел общей погрешности есть сумма модулей отдельных составляющих.

Дата добавления: 2014-01-20