
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Эквивалентные схемы механических поступательных подсистем
|
|
|
|
Механические системы
Фазовыми переменными в механических поступательных системах являются силы и скорости.
Переменной типа потока является сила F, переменной типа потенциала- скорость V. Простейшие элементы: трение K, масса m, упругость С, компонентные уравнения которых:
F= kV, F=m , V=
, V=
и источники силы и скорости с компонентными уравнениями:
F=F(Z), V=V(Z), где в качестве Z может фигурировать время или фазовая переменная.
Компонентное уравнение элемента упругости может быть получено как из уравнения линейной пружины, так и из закона Гука. Для линейной пружины справедливо уравнение: F=C*X, где X - взаимное смещение концов пружины, путем дифференцирования уравнения по времени получим 3-е компонентное уравнение.
Для упругой балки справедливо уравнение Гука
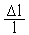 =
=  , где Δl- относительное удлинение, l - длина, S - площадь поперечного сечения, E - модуль Юнга. Дифференцируя по времени получим:
, где Δl- относительное удлинение, l - длина, S - площадь поперечного сечения, E - модуль Юнга. Дифференцируя по времени получим:
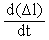 =
= , или V=
, или V= , где C=
, где C=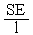 .
.
Нетрудно заметить наличие аналогий между электрической и механической системами. Так, токам и напряжениям в первой из них соответствуют силы (либо моменты) и скорости механической системы, компонентным уравнениям и фигурирующим в них параметрам 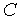 и
и 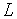 — уравнения и параметры
— уравнения и параметры 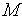 и
и  , очевидна аналогия и между топологическими уравнениями. Далее параметры
, очевидна аналогия и между топологическими уравнениями. Далее параметры 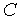 и
и 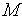 будем называть емкостными (емкостного типа), параметры
будем называть емкостными (емкостного типа), параметры 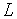 и
и  — индуктивными (индуктивного типа), а параметры
— индуктивными (индуктивного типа), а параметры 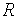 и
и  — резистивными (резистивного типа).
— резистивными (резистивного типа).
Имеется и существенное отличие в моделировании электрических и механических систем: первые из них одномерны, а процессы во вторых часто приходится рассматривать в двух- (2D) или трехмерном (3D) пространстве. Следовательно, при моделировании механических систем в общем случае в пространстве 3D нужно использовать векторное представление фазовых переменных, каждая из которых имеет шесть составляющих, соответствующих шести степеням свободы.
Условные изображения элементов на эквивалентных схемах представлены на рис.

|
Рис. 1.
Топологические уравнения:
а) уравнение равновесия  (принцип Даламбера)- сумма сил инерции, активных и реактивных равна 0.
(принцип Даламбера)- сумма сил инерции, активных и реактивных равна 0.
б) уравнение непрерывности 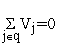 (принцип сложения ско ростей) Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости самой подвижной системы отсчета относительно неподвижной системы.
(принцип сложения ско ростей) Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости самой подвижной системы отсчета относительно неподвижной системы.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 694; Нарушение авторских прав?; Мы поможем в написании вашей работы!