
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Представление топологических уравнений
|
|
|
|
Известен ряд методов формирования ММС на макроуровне. Получаемые с их помощью модели различаются ориентацией на те или иные численные методы решения и набором базисных переменных, т.е. фазовых переменных, остающихся в уравнениях итоговой ММС. Общим для всех методов является исходная необходимость получения информации об эквивалентной схеме и соединении элементов в узлы.
При записи топологических уравнений удобно использовать промежуточную графическую форму — представление модели в виде эквивалентной схемы, состоящей из двухполюсных элементов. Общность подхода при этом сохраняется, так как любой многополюсный компонент можно заменить подсхемой из двухполюсников. В свою очередь эквивалентную схему можно рассматривать как направленный граф, дуги которого соответствуют ветвям схемы.
Граф, подграф, сурграф (подграф, включающий все вершины графа), нормальное дерево (фундаментальное дерево с ветвями, рассматриваемыми в последовательности E, C, R, L, J) - эти понятия из теории графов понадобятся при рассмотрении. Направления потоков в ветвях выбираются произвольно (если реальное направление при моделировании окажется противоположным, то это приведет лишь к отрицательным численным значениям потока). Пример некоторой простой эквивалентной схемы и соответствующего ей графа приведен на рис. 1,a. Для конкретности и простоты изложения на рис. 1,a использованы условные обозначения, характерные для электрических эквивалентных схем, по той же причине далее в этом параграфе часто применяется электрическая терминология. Очевидно, что поясненные выше аналогии позволяют при необходимости легко перейти к обозначениям и терминам, привычным для механиков.
Для получения топологических уравнений все ветви эквивалентной схемы разделяют на подмножества хорд и ветвей дерева. Имеется в виду фундаментальное дерево (покрывающее дерево), т.е. подмножество из  дуг, не образующее ни одного замкнутого контура, где
дуг, не образующее ни одного замкнутого контура, где  — число вершин графа (узлов эквивалентной схемы). На рис. 1,б показан граф эквивалентной схемы рис. 1,a, толстыми линиями выделено одно из возможных покрывающих деревьев.
— число вершин графа (узлов эквивалентной схемы). На рис. 1,б показан граф эквивалентной схемы рис. 1,a, толстыми линиями выделено одно из возможных покрывающих деревьев.

|
Рис. 1. Эквивалентная схема и соответствующий ей граф
Выбор дерева однозначно определяет вектора напряжений  и токов
и токов  хорд, напряжений
хорд, напряжений  и токов
и токов  ветвей дерева и приводит к записи топологических уравнений в виде
ветвей дерева и приводит к записи топологических уравнений в виде
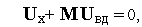
| (1) |

| (2) |
где  — матрица контуров и сечений,
— матрица контуров и сечений,  — транспонированная
— транспонированная  -матрица.
-матрица.
 - матрица несет информацию в заложенной структуре о порядке соединения элементов. Число строк соответствует числу хорд, число столбцов равно числу ветвей дерева.
- матрица несет информацию в заложенной структуре о порядке соединения элементов. Число строк соответствует числу хорд, число столбцов равно числу ветвей дерева.  -матрица формируется следующим образом. Поочередно к дереву подключаются хорды. Если при подключении к дереву
-матрица формируется следующим образом. Поочередно к дереву подключаются хорды. Если при подключении к дереву 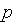 -й хорды
-й хорды 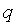 -я ветвь входит в образовавшийся контур, то элемент
-я ветвь входит в образовавшийся контур, то элемент  матрицы равен
матрицы равен  при совпадении направлений ветви и подключенной хорды,
при совпадении направлений ветви и подключенной хорды,  при несовпадении направлений. В противном случае
при несовпадении направлений. В противном случае  .
.
Для схемы на рис. 1,б  -матрица представлена в виде табл. 1.
-матрица представлена в виде табл. 1.
Таблица 1
| Обозначение | Ветвь C1 | Ветвь C2 | Ветвь C3 |
| Хорда R1 |  1 1
| ||
| Хорда R2 |  1 1
| ||
| Хорда R3 |  1 1
| ||
| Хорда R4 |  1 1
| +1 | +1 |
| Хорда J | +1 |
Отметим, что в случае электрических и гидравлических систем уравнения (1) представляют собой уравнения напряжений Кирхгофа для контуров, образованных поочередным подключением каждой из хорд в отдельности к дереву, а уравнения (2) — уравнения токов Кирхгофа для сечений ветвей дерева.
Второй шаг – решение системы полученных ОДУ+АУ тем или иным способом.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 851; Нарушение авторских прав?; Мы поможем в написании вашей работы!