Метод узловых потенциалов

Уравнения, составляемые по этому методу, называются узловыми уравнениями. Их число значительно сокращается по сравнению с числом уравнений в методе уравнений Кирхгофа, за счет применении первого закона Кирхгофа и обобщенного закона Ома.

В качестве неизвестных они содержат потенциалы узлов, причем один из них задается заранее – обычно принимается равным нулю. Рационально заземлять узел, в котором сходится максимальное число ветвей.

По найденным значениям потенциалов с помощью закона Ома для участка цепи с источником ЭДС затем находят токи в ветвях. Таким образом, число неизвестных потенциалов, а следовательно, и число уравнений равно 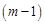, т.е. числу ветвей дерева d.

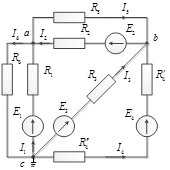
Рис. 4.

Пусть имеем схему по рис. 4, в которой примем 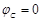. Допустим, что 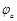и известны. Тогда значения токов на основании закона Ома для участка цепи с источником ЭДС

,

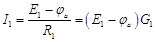
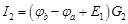
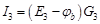
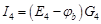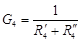
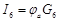
Запишем уравнение по первому закону Кирхгофа для узла а:

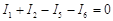
и подставим значения входящих в него токов, определенных выше:

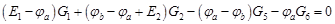
Сгруппировав соответствующие члены, получим:

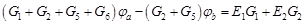
Аналогично можно записать для узла b:

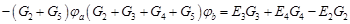
Система уравнений по методу узловых потенциалов может быть составлена формальным путем. При этом необходимо руководствоваться следующими правилами:

1. В левой части i- гоуравнения записывается со знаком “+”потенциал φ_i i- го узла, для которого составляется данное i- е уравнение, умноженный на сумму проводимостей G_ii ветвей, присоединенных к данному i- му узлу, и со знаком “–” потенциал φ_k соседних узлов, каждый из которых умножен на сумму проводимостей G_ik ветвей, присоединенных к i- му и k- му узлам.

Из сказанного следует, что все члены φ_iG_ii, стоящие на главной диагонали в левой части системы уравнений, записываются со знаком “+”, а все остальные – со знаком “-”, причем G_ik = G_ki. Последнее равенство обеспечивает симметрию коэффициентов уравнений относительно главной диагонали.

2. В правой части i- гоуравнения записывается так называемый узловой ток J_i, равный сумме произведений ЭДС ветвей, подходящих к i- му узлу, и проводимостей этих ветвей. При этом член суммы записывается со знаком “+”, если соответствующая ЭДС направлена к i- му узлу, в противном случае ставится знак “-”. Если в подходящих к i- му узлу ветвях содержатся источники тока, то знаки токов источников токов, входящих в узловой ток простыми слагаемыми, определяются аналогично.

Составленная таким образом система уравнений имеет следующий обобщенный вид:

где G ₁₁, G ₂₂,..., G_mm – собственные проводимости узлов, равные сумме проводимостей ветвей, соединяющихся в соответствующем узле;

G ₁₂, G ₂₁, G ₁₃,... – общие проводимости между двумя узлами, равные сумме проводимостей ветвей, соединяющих эти узлы;

J ₁₁, J ₂₂,..., J_mm – узловые токи, равные алгебраической сумме произведений проводимостей активных ветвей на ЭДС этих ветвей и токов источников тока, соединяющихся в этом узле.

С положительным знаком берут ЭДС и токи, направленные к узлу.

Составим систему уравнений для схемы на рис. 3.2:

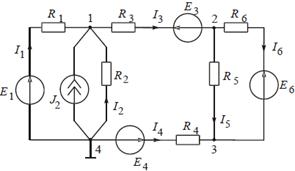
Рис. 3.2

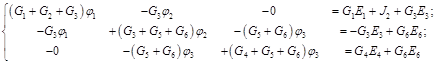
Решением системы уравнений определим потенциалы узлов. Затем рассчитаем токи ветвей по закону Ома:

I ₁ = G ₁(φ ₄ − φ ₁ + E ₁ ) = G ₁(− φ ₁ + E ₁),

так как φ ₄ = 0,

I ₂ = − G ₂ φ ₁;

I ₃ = G ₃(φ ₁ − φ ₂ − E ₃);

I ₄ = G ₄(− φ ₃ + E ₄);

I ₅ = G ₅ (φ ₂ − φ ₃ );

I ₆ = G ₆ (φ ₂ − φ ₃ − E ₆ ).

На основе проведенного рассмотрения можно сформулировать процедуру расчет электрической цепи методом узловых потенциалов.

Порядок расчета:

1. Произвольно выбрать направления всех токов в ветвях на исходной схеме.

2. Пронумеровать узлы на исходной схеме. Положить равным нулю потенциал последнего узла. Определить количество уравнений N системы уравнений

N=N_у – N_и – 1,

где N_у – число узлов;

N_и – число ветвей, содержащих только идеальные источники ЭДС.

Решить систему уравнений относительно потенциалов узлов j_i

,

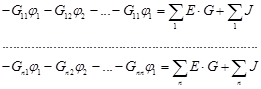где G_ss – сумма проводимостей ветвей, присоединенных к узлу s, не содержащих источников тока;

G_sq – сумма проводимостей ветвей, непосредственно соединяющих узел s с узлом q;

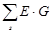– алгебраическая сумма произведения ЭДС ветвей, примыкающих к узлу s, на их проводимости. Это произведение берется со знаком "плюс", если ЭДС Е направлено к узлу s, иначе "минус";

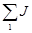– алгебраическая сумма источников тока, присоединенных к узлу s. Ток J берется со знаком "плюс", если он направлен к узлу s, иначе "минус".

4. Вычисляют токи из обобщенного закона Ома или первого закона Кирхгофа.

Дата добавления: 2014-01-20