Метод построения областей устойчивости- D-разбиение

Условие устойчивости

Необходимым и достаточным условием устойчивости САУ (в линейном приближении) является то, что корни (комплексные) имеют отрицательную действительную часть или же в случае действительных корней – отрицательную. Тогда для практических целей можно решать 2 задачи:

1 задача: заданы все параметры системы, кроме искомых (выбранных). Необходимо определить, при каких значениях искомых параметров система устойчива.

2 задача: заданы все параметры системы. Определить, устойчива ли система при этих значениях параметров.

1 задача решается построением областей устойчивости; 2 задача – с использованием критериев устойчивости.

Вычисление корней характеристических уравнений высоких порядков – задача трудоемкая. Поэтому устойчивость исследуют с помощью специально введенных оценок, связанных с коэф. характеристического уравнения и называемых критериями устойчивости.

Предположим, имеется система, описываемая дифференциальным уравнением, характеристическое уравнение которой имеет следующий вид:

a_npⁿ+a_n-1p^n-1+…+a₁p+a₀=0

Примем, что в данном уравнении все коэффициенты известны, кроме а₁ и а₀. Тогда, варьируя неизвестными коэффициентами а₁ и а₀, можно построить в плоскости параметров характеристику, в которой выделяется область устойчивости, за этой границей неустойчивая область.

Уст.обл.

Если известны три параметра:

a₁

0 a₀

a₂

Для “n” параметров – это называется гиперплоскость.

Если в результате подобного построения системы можно ввести в область устойчивости, то говорят, что она структурно устойчива. С практической точки зрения, когда простейшая локальная система регулирования из объекта и регулир. устройства, удобно искать область устойчивости в пространстве параметров, определяющих динамические свойства системы регулирования, а конкретно параметры регулятора.

W_об(р)

X(t) y(t)

W_p(p)=K_p+K_p/T_up

К_р и Т_и – параметры настройки регулятора.

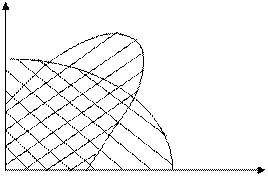K_p/T_u

2

1

0 K_P

W_c(p)=W_об(p)/(1+W_об(p)∙W_p(p))

Для систем регулирования в качестве варьируемых параметров принимают параметры К_р – коэффициент передачи регулятора и Т_и – коэффициент времени ввода интегральной составляющей в алгоритме регулирования.

Тогда получаем область устойчивости реальной системы регулирования с заданным значением регулирования и позволяющей выделить в этой области наибольшее перспективное (качественное) сочетание выбранных параметров настройки.

Метод выделения областей устойчивости в пространстве коэффициентов был предположен ученым Неймарком и получил название D-разбиение.

Дата добавления: 2014-01-20