Критерий устойчивости Михайлова

Для использования этого критерия необходимо также иметь математическое описание системы в виде дифференциального уравнения, а значит можно перейти через преобразование Лапласа к алгебраической форме в виде характеристического уравнения, которое имеет такой же вид, как и для критерия Гауса-Гурвица.

Однако, оценку устойчивости согласно данному критерию ведут в частотной области.

Тогда предположим, имеется:

a_npⁿ+a_n-1p^n-1+…+a₁p+a₀=0 | p=iω(замена)

Заменив р на iω, мы переходим в частотную область с комплексной переменной:

М(iω)= a_n(iω)ⁿ+a_n-1(iω)^n-1+…+a₁(iω)+a₀

Вектор Михайлова:

М(iω)=R(ω)+ iI(ω)

i=

i²= - 1

i³= - = - 2

i⁴=1

Меняя величину ω от 0 до ∞ можно заметить, что вектор Михайлова М(iω) будет вращаться против часовой стрелки около начала координат в комплексной плоскости, меняя свою величину.

На основании этого, согласно критерию Михайлова, система, описываемая линейным дифференциальным уравнением с постоянными коэффициентами, будет устойчива, если годограф вектора Михайлова с изменением частоты от 0 до ∞ обходит последовательно в положительном направлении (против часовой стрелки), нигде не обращаясь в 0, n квадрантов, где n-порядок характеристического уравнения системы (поворот на 1 квадрант – это поворот на π/2).

В случае, когда вектор Михайлова проходит через 0, на этой частоте система находится на границе устойчивости.

Необходимым и достаточным условием устойчивости системы по критерию Михайлова является наличие у многочленов действительных корней и их перемножаемость.

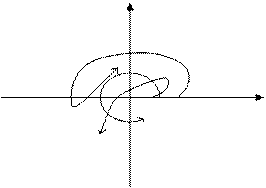iI(ω)

неустойчива

R(ω)

на грани устойчивости устойчива

Пример:

p⁴+5p³+3p²+2p+0,03=0

М(iω)=(iω)⁴+5(iω)³+3(iω)²+2(iω)+0,03

М(iω)=ω⁴-5(iω)³-3(iω)²+2ω+0,03

M(iω)=R(ω)+iI(ω)

Наиболее характерными точками для оценки устойчивости являются пересечение вектора Михайлова осей комплексной плоскости.

Дата добавления: 2014-01-20