Передача энергии при парном взаимодействии

Элементарные процессы в плазме.

Лекция 2.

Наиболее важными характеристиками плазмы являются температура электронов Т_е и плотность электронов n_e.

Частицы в плазме непрерывно взаимодействуют между собой. При этом возможны взаимодействия между любыми группами частиц, а также взаимодействие частиц с окружающей средой (стенки разрядной камеры, кванты света от внешнего источника и т.д.). Процессы в плазме, в которых участвуют только две частицы, получили название элементарных (парных) взаимодействий. В плазме происходит множество различных видов элементарных взаимодействий (возбуждение, ионизация, кулоновское рассеяние и др.). Скорость протекания этих процессов и их влияние на параметры плазмы различны, при этом каждый элементарный процесс характеризуется своей вероятностью.

В общем случае различают упругие (без изменения внутренней энергии частиц) и неупругие (с изменением внутренней энергии) взаимодействия частиц. Важным является вопрос о передаче энергии при взаимодействии двух частиц.

Упругое соударение (взаимодействие)

Рассмотрим случай (рис. 2.1), когда частица массой m, имеющая скорость u, сталкивается с неподвижной частицей массой М. После упругого взаимодействия частица массой m приобретает скорость u^¢ под углом j к начальному направлению движения (ось х), а частица массой М приобретает скорость V^¢, направленную под углом e к оси х. Такое взаимодействие описывается законами сохранения импульса и энергии:

По оси хmu = mu^¢cosj + M V^¢cose, (2.1)

По оси y 0 = mu^¢sinj + M V^¢ sine, (2.2)

mu²/2 = mu^¢2/2 + M V^¢2/2. (2.3)

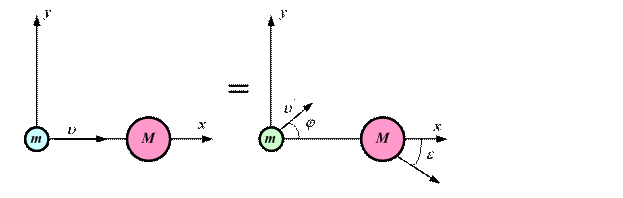
Рис. 2.1. Упругое рассеяние двух частиц

Возводя в квадрат уравнения (2.1) и (2.2), предварительно перенеся в левую часть mu^¢cosj и mu^¢sinj, складывая эти уравнения почленно с учетом того, что sin²j + cos²j = 1 и sin²e+ cos²e = 1, вычитая из полученного соотношения уравнение (2.3), предварительно умножив его левую и правую части на 2М, получаем квадратное уравнение вида

(1 + M/m) u^¢2 - 2u^¢u cosj + (1 - M/m)u² = 0. (2.4) Решение этого уравнения имеет вид

u^¢ = {2u cosj +[4u² cos²j + 4(1 – M²/m²)u²]^1/2}/[2(1 + M/m)], (2.5) или u^¢ =u[m/(M + m)][cosj + (M²/m² – sin²j)^1/2]. (2.6)

Ограничимся рассмотрение случая, когда m << M (например, при взаимодействии электрона с атомом или ионом). Тогда

u^¢ =u[m/(M + m)][cosj + (M/m)]. (2.7)

D u = u – u ^¢ = u[m/(M + m)][1 – cosj]. (2.8)

Поскольку m << M, то D u << u и u + u ^¢ = 2u. Умножая (2.8) на u + u ^¢, и принимая во внимание, что кинетическая энергия частицы массой m до взаимодействия E_k = mu²/2, определим изменение этой энергии D Е следующим образом:

D Е = E_k[2m/(m + M)] [1 – cosj]. (2.9)

Усредняя по всем возможным значениям угла j, окончательно получаем

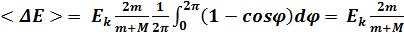. (2.10)

Из соотношения (2.10) следует, что при упругом взаимодействии легкой и тяжелой частиц передача кинетической энергии последней минимальна. Например, при столкновении электрона с атомом аргона (m/M = 1/80000), D Е = E_k/ 40000. Таким образом, электрон при столкновении с атомами и ионами практически не передает ему никакой энергии, если это столкновение упругое.

Неупругое взаимодействие (соударение)

Ограничимся рассмотрением, так называемого, лобового столкновения, когда движение каждой из частиц происходит вдоль оси х (рис. 2.2).

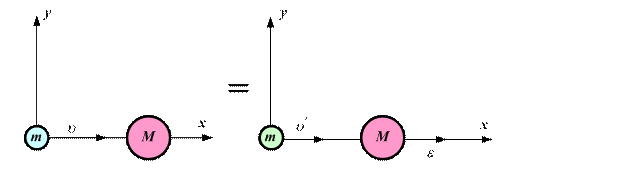Рис. 2.2. Неупругие столкновения двух частиц.

Для этого случая законы сохранения энергии и импульса запишутся в виде

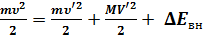, (2.11)

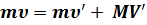, (2.12) где D Е_вн – изменение внутренней энергии частицы. Выражая из (2.12) V и подставляя его в (2.11), получаем для D Е_вн

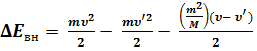. (2.13)

Легко показать, что зависимость D Е_вн от 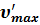, при котором изменение внутренней энергии максимально

Дата добавления: 2014-01-20