Определение линейного оператора

Лекция №4. Линейные операторы

В общем курсе математического анализа изучаются функции одного или нескольких вещественных переменных. Например, в случае функции трех вещественных переменных можно говорить о функции, аргументом которой является свободный вектор трехмерного пространства. Ниже мы будем изучать функции, аргументом которых будет вектор произвольного линейного пространства. Причем мы рассмотрим простейшие типы таких функций, а именно линейные функции. При этом линейные числовые функции векторного аргумента, т.е. функции, значения которых суть числа называют линейными формами (функционалами), а линейные векторные функции векторного аргумента, значения которых суть векторы называют линейными операторами (отображениями, преобразованиями).

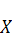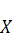Пусть заданы два различных непустых множества и , элементы которых будем обозначать буквами соответственно 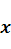и .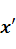

Определение 1. Правило (закон), по которому любому элементу 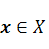ставится в соответствие единственный элемент 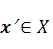называется оператором, действующим из 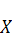в .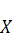

Если оператор обозначить буквой 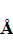,то результат 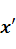его применения к элементу 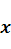записывают в виде

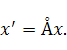
Множество 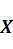называется областью определения оператора 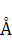, элемент 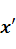при этом называется образом элемента 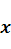, а сам элемент 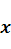– прообразом элемента 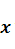. Совокупность всех образов называется областью значений оператора 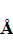. Если каждый элемент 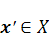′ имеет только один прообраз, то оператор 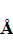называется взаимно однозначным. Множество элементов 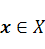, удовлетворяющих равенству 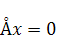, называются ядром оператора .

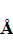Будем в дальнейшем под 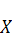и 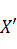понимать линейное пространство .

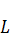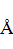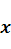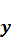Определение 2. Оператор называется линейным, если для любых двух векторов и из 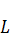и произвольного числа 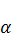выполняются условия:

1. 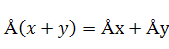(аддитивность);

2. 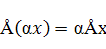(однородность).

Покажем, что любой линейный оператор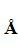можно задать, указав некоторый набор чисел. Действительно, выберем в пространстве 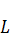некоторый базис 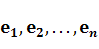и обозначим через x произвольный вектор из 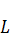, а через 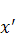его образ, то есть

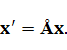
Выпишем разложения векторов 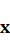и 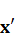по выбранному базису

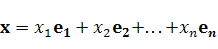
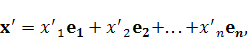
где 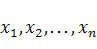и 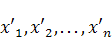координаты векторов соответственно 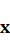и 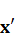в базисе 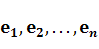. Если подставить первое из последних равенств в правую часть предыдущего равенства и использовать линейность оператора, то получим

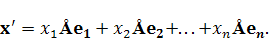
Векторы 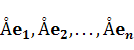принадлежат пространству 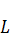и, следовательно, в выбранном базисе можем написать

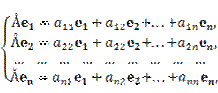
где 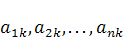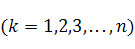‑ координаты вектора 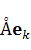в базисе 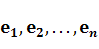. Подставив последние равенства в правую часть предыдущего равенства и, используя разложение вектора 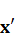в выбранном базисе, получим

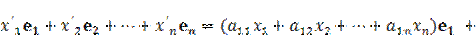
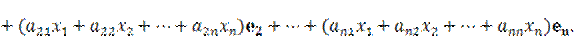
Используя единственность разложения вектора в данном базисе, приравняем коэффициенты при базисных векторах в левой и правой частях последнего равенства. При этом получим

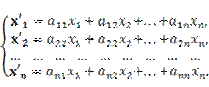(4.1)

Непосредственно из формулы (4.1) видно, что правило перехода от вектора 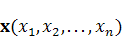к вектору 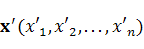или от точки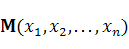к новой точке 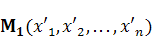полностью определяется квадратной матрицей

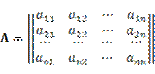, (4.2)

составленной из коэффициентов формул (4.1).

Определение. Матрица 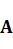называется матрицей линейного оператора 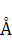в базисе 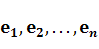, а сам этот оператор называют оператором с матрицей 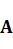в базисе .

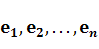Если ввести в рассмотрение одностолбцовую матрицу

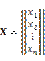(4.3)

и вычислить произведение матриц

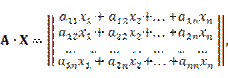
то получим одностолбцовую матрицу, элементами которой являются суммы, стоящие в правых частях равенств (4.1).

Если же ввести в рассмотрение матрицу

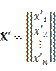(4.4)

и воспользоваться понятием равенства матриц, то система (4.1) может быть записана в виде

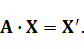(4.5)

Дата добавления: 2014-01-20