
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определители n-го порядка
|
|
|
|
Определителем 3-го порядка называется величина, обозначаемая символом
Определители 2-го и 3-го порядков
Определителем 2-го порядка называется величина, обозначаемая символом  , и вычисляемая по формуле
, и вычисляемая по формуле 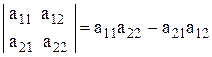 .
.
 , и вычисляемая по формуле
, и вычисляемая по формуле 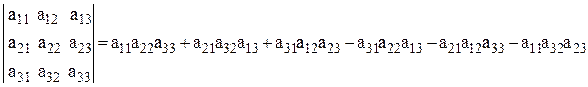 (*)
(*)
Формула (*) получается по следующей формуле:

Определитель 4-го порядка состоит из 4 строк и 4 столбцов, определитель 5-го порядка состоит из 5 строк и 5 столбцов и т.д., соответственно определитель n-го порядка состоит из n строк и n столбцов:
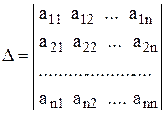 - определитель n-го порядка,
- определитель n-го порядка,
числа 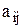 - элементы определителя (индекс i - номер строки, индекс j –номер столбца, на пересечении которых стоит данный элемент). (
- элементы определителя (индекс i - номер строки, индекс j –номер столбца, на пересечении которых стоит данный элемент). (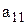
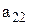 ....
....  ) – главная диагональ, а (
) – главная диагональ, а (
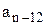 ....
....  ) - побочная диагональ.
) - побочная диагональ.
Вычисление определителей 4-го и последующих порядков можно свести к вычислению определителей 2-го и 3-го порядков с помощью следующих свойств определителей:
Свойства определителей:
- величина определителя не изменится от замены строк столбцами.
- величина определителя от перестановки двух любых строк (столбцов) меняет свой знак на противоположный.
- умножение всех элементов произвольной строки(столбца) определителя на число
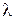 равносильно умножению числа
равносильно умножению числа 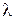 на величину определителя.
на величину определителя. - определитель со строкой (столбцом), состоящей только из нулей, равен нулю.
- если все элементы некоторой строки (столбца) состоят из двух слагаемых, то определитель равен сумме двух определителей, в одном из которых элементами этой строки (столбца) являются первые слагаемые, во втором – вторые, а остальные элементы такие же, как и в данном определителе.
- определитель равен нулю, если элементы каких-нибудь двух строк (столбцов) пропорциональны.
- величина определителя не изменится, если к элементам одной строки (столбца) прибавить элементы другой строки (столбца), умноженные на произвольное число
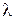 .
.
Последнее свойство определителей сформулируем, введя предварительно понятие алгебраического дополнения элемента определителя.
Алгебраическим дополнением  элемента
элемента 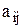 определителя n-го порядка называется произведение
определителя n-го порядка называется произведение  на определитель (n-1)-го порядка, получающийся вычеркиванием в данном определителе строки и столбца, на пересечении которых стоит элемент
на определитель (n-1)-го порядка, получающийся вычеркиванием в данном определителе строки и столбца, на пересечении которых стоит элемент 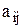 .
.
8. Определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения, т.е.
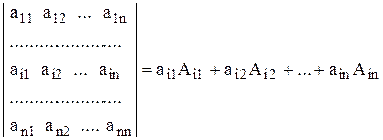 (**)
(**)
Это свойство позволяет свести вычисление определителя n- го порядка к вычислению определителей (n-1)-го порядка. Если некоторые элементы строки (столбца) равны нулю, то в сумме (**) соответствующие им слагаемые равны нулю и потребуется вычислять не n определителей (n-1)-го порядка, а меньше.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 590; Нарушение авторских прав?; Мы поможем в написании вашей работы!