Точки системы могут иметь те или иные стеснения своих движений, называемых связями

Механической системой называется множество материальных точек, выделенных для изучения и объединенных по некоторому принципу (Солнечная система, механические устройства и механизмы).

1Свободная точка, не имеющая связей, имеет три степени свободы, т.е. для описания ее положения необходимо задать три параметра x(t), y(t), z(t).

3. На свободную точка наложена одна связь – мы удерживаем ее с помощью невесомого стержня длины R. Один конец стержня шарнирно закреплен в точке О. В этом случае координаты точки обязаны подчиняться уравнению x² + y² + z²=R и мы говорим, что на точку наложена стационарная удерживающая связь, у нее осталось две степени свободы (точка может находиться на поверхности сферы радиуса R и ее положение можно описать с помощью двух параметров, например двух углов).

В общем случае мы имеем механическую систему из n точек, каждая точка имеет три степени свободы, а вся механическая система, если на нее не наложено никаких связей, имеет 3n степеней свободы.

Ограничения на движение точек системы (связи) заданы независимыми между собой уравнениями:

f_j(x₁,y₁,z₁…..x_n,y_n,z_n) = 0 (j = 1,2….s)

Если число связей s равно 3n, то эти уравнения определяют 3n координат, система может иметь одно или несколько определенных положений и перемещаться не будет. Для возможности перемещения системы должно выполняться условие k = 3n – s > 0. Число k называют числом степеней свободы системы.

Пусть к материальной точке М приложена сила F. Предположим, что точке М сообщено некоторое бесконечно малое не противоречащее уравнениям связей перемещение 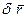. Это перемещение назовем возможным в отличие от действительного 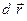, которое точка совершает на самом деле под действием приложенных сил.

Элементарной работой силы F на возможном перемещении 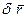называют величину

У нас есть система точек M_i с координатами (x_i,y_i,z_i) и действующие на них силы 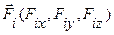(i=1,2…n). Точки системы стеснены некоторыми связями. По аксиоме о связях их действие можно заменить действием сил реакций 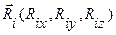(i=1,2…n). То есть, добавив к силам F_i все реакции R_i систему точек можно мыслить свободной от связей, вызывающих реакции R_i.

Определение. Идеальными называются связи, работа сил реакций (i=1,2…n) которых на любых возможных при этих связях перемещениях равна нулю, то есть

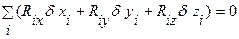
Сформулируем основной принцип аналитической статики для систем с идеальными удерживающими стационарными связями. Система точек находится в состоянии равновесия, значит сумма проекций сил на все оси декартовой системы координат должны быть равны нулю:

F_ix+R_ix=0; F_iy+R_iy=0; F_iz+R_iz=0; (I=1,2…n)

Отсюда мы можем определить R_ix,R_iy,R_iz и подставив в уравнение определения для идеальных связей получить выражение:

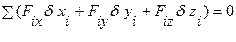
справедливое для произвольных возможных перемещений в положении равновесия рассматриваемой механической системы. Это и есть необходимое и достаточное условие равновесия механической системы, которое называется принципом возможных перемещений. Принцип возможных перемещений может быть взят за основу всех положений статики взамен набора аксиом, которые мы использовали с самого начала для вывода наших результатов.

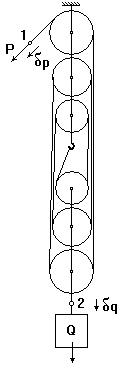
Пример 1. Рассмотрим полиспаст, одно из простейших механических устройств, которое давно известно человечеству, как и устройства вроде рычага и клина.

С точки зрения аналитической статики полиспаст представляет собой механическую систему, состоящую из двух точек 1 и 2, к которым приложены силы P и Q, все прочее относится к реализации связи между этими двумя точками.

Для нашего случая принцип возможных перемещений записывается так:

Pdp + Qdq = 0,

Здесь dp и dq – возможные перемещения точек 1 и 2, которые не являются независимыми. Легко установить соотношение dp = -6 dq и после подстановки в вышеприведенную формулу получить:

P = Q/6.

Это означает, что с помощью приведенной на рисунке конструкции полиспаста для удержания в равновесии груза весом Q необходимо приложить в 6 раз меньшую силу P.

Пример 2. Рассмотрим гибкую однородную тонкую тяжелую нить, закрепленную в точках A и B, длина нити – l

l² > x²_B + y²_B

Нить нерастяжимая, ds вдоль длины нити не меняется.

f º dx² + dy² + dz² – ds² = 0

Рассматриваем плоский случай параллельных сил тяжести: dx² + dy² – ds² = 0

Дата добавления: 2014-01-20