Обобщенные силы

УРАВНЕНИЯ ЛАГРАНЖА 2-ГО РОДА

Пусть система состоит из N точек, тогда ее положение в пространстве определяется в каждый момент времени 3 N координатами точек системы, например, декартовыми х_k, у_k,, z_k. Пусть на систему наложено п голономных связей. На 3 N координат наложено п уравнений связи, тогда независимых координат будет К = 3N-n.

Любые К координат можно задать независимо, остальные определятся из уравнений связей. Введем К обобщенных координат q₁, q₂, …,q_K каждая из которых зависит от декартовых координат. В общем случае они могут зависеть от всех декартовых координат точек системы, т.е.

q_i=q_i(x_k, y_k, z_k)

здесь i = 1,2,..., К; k = 1,2,... ,N

Можно выразить декартовые координаты через обобщенные, при условии разрешимости системы, т.е. получить

x_k=x_k(q₁, q₂, …,q_K), y_k=y_k(q₁, q₂, …,q_K), z_k=z_k(q₁, q₂, …,q_K),

Элементарная работа внешних сил, приложенных к точкам системы, на возможных перемещениях точек этой системы определяется следующим выражением

.

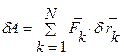Пусть голономная система имеет К степеней свободы и, следовательно, ее положение можно определять обобщенными координатами: q₁, q₂, …,q_K.

Тогда, имея в виду, что 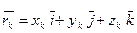и получаем, что .

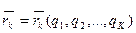Тогда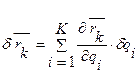

Подставляя в выражение для элементарной работы, можно записать

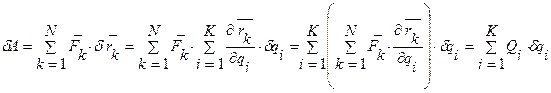
где скалярная величина

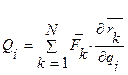
называется обобщенной силой, отнесенной к обобщенной координате q_i.

Для вычисления обобщенной силы Q_i необходимо дать системе возможное перемещение δq_i и вычислить возможную работу всех сил на этом перемещении, тогда сомножитель перед δq_i и будет представлять обобщенную силу Q_i.

Обобщенную силу можно переписать

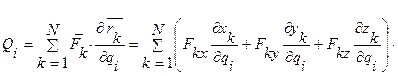
Приступим к выводу дифференциальных уравнений движения голономной системы в обобщенных координатах: q₁, q₂, …,q_K.. Будем исходить из общего уравнения динамики

,

.

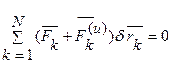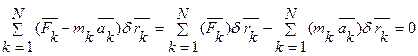Первое слагаемое запишем через обобщенную силу:

,.

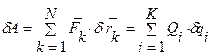Запишем второе слагаемое через обобщенные координаты. Имеем

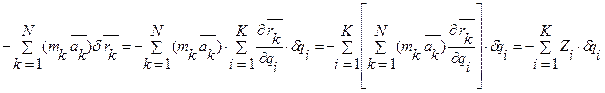
Распишем Z_i.

,

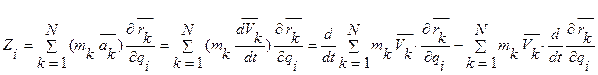в чем легко убедиться непосредственным дифференцированием.

Докажем, что выполняется следующее соотношение:

.

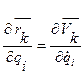Действительно, 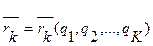, тогда

.

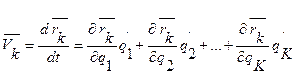Так как множители 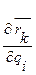(i = 1,2,..., К) зависят только от обобщенных координат (и не зависят от обобщенных скоростей), то, дифференцируя равенство скорость по обобщенным скоростям, получаем, что

,

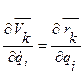следовательно, равенство доказано.

Далее, имеем

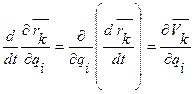
Возвращаясь к формуле для Z_i и подставляя в нее полученные тождества, имеем

.

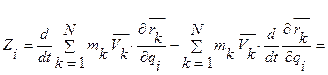
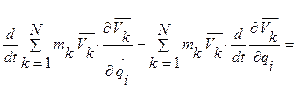
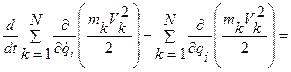
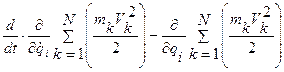Здесь V_k - скорость k-ой точки;

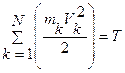- кинетическая энергии механической системы.

Итак, получили, что

.

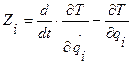Тогда общее уравнение динамики в обобщенных координатах имеет вид:

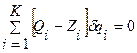
Так как q_i - независимые координаты, томожет иметь место только тогда, когда все коэффициенты при δq_i, в этом уравнении равны нулю. Поэтому общее уравнение динамикиэквивалентно системе уравнений Z_i=Q_i (i = 1,2,...,К), которые могут быть записаны в следующем виде:

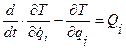, (i=1, 2, …, K)

Эти уравнения носят название уравнений Лагранжа второго рода.

Величина 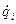- называется обобщенной скоростью; 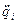- обобщенным ускорением.

Уравнения Лагранжа второго рода образуют систему из К обыкновенных дифференциальных уравнений второго порядка с К неизвестными. Напомним, что К - число степеней свободы рассматриваемой механической системы.

Итак, число уравнений Лагранжа второго рода равно числу степеней свободы системы.

Уравнения Лагранжа дают единый и достаточно простой метод решения задач динамики и для простых и для сложных механических систем.

При составлении уравнений Лагранжа для заданной механической системы рекомендуется следующая последовательность действий:

- установить число степеней свободы системы и выбрать обобщенные координаты;

- изобразить систему в произвольном положении (обобщенные координаты должны быть положительными) и показать на рисунке все действующие на систему внешние силы;

- вычислить кинетическую энергию системы в ее произвольном движении и выразить ее через обобщенные координаты q_i, и обобщенные скорости ;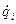

- выполнить предусмотренные уравнениями Лагранжа операции дифференцирования кинетической энергии системы;

- вычислить обобщенные силы, последовательно задавая элементарные положительные перемещения только соответствующей обобщенной координате;

- подставить все полученные выражения в уравнениях Лагранжа и решить полученную линейную систему К уравнений относительно К неизвестных обобщенных ускорений: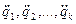

Пример 1. Твердое тело вращается вокруг неподвижной оси z под действием вращающего момента М_вр. Составить дифференциальное уравнение вращения твердого тела.

Решение. В качестве обобщенной координаты выберем угол поворота φ. Соответствующая обобщенная сила равна

.

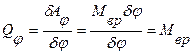Кинетическая энергия вращающегося тела

.

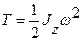Уравнение Лагранжа

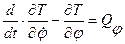
после подстановки

, ,

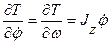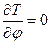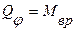
Дата добавления: 2014-01-20