Описание в частотной области

Для исследования частотной характеристики на вход подают синусоидальную последовательность x(t_i) = x₀sin(wt_i). Если система линейна, на выходе также возникнет синусоида. Отношение амплитуд, как и в аналоговых фильтрах, равно значению передаточной функции. Линейность цифрового фильтра следует из линейности дифференциального уравнения. Таким образом, согласно формуле (4.1), фильтр на рис. 4.1 линеен.

Передаточная функция может быть получена, как и в случае аналогового фильтра, расчетом с использованием комплексных переменных. Найдем частотную характеристику элемента задержки. Для гармонического входного сигнала

получается гармонический выходной сигнал

и с учетом jw=р передаточная функция имеет вид

Эта функция периодическая с периодом w₀=2p/T₀=2pf₀. Здесь f₀ – тактовая частота. Введем обозначение

и получим из формулы (4.2) передаточную функцию элемента задержки на один такт в виде

Из ранее изученных курсов (ТОЭ, МАРЭС) известно, что связь передаточной функции А(р), входного сигнала, имеющего произвольную зависимость от времени и сигнала на выходе четырехполюсника с помощью преобразования Лапласа может быть представлена в виде

Это соотношение справедливо и для цифровых систем. Для числовых последовательностей его можно упростить с помощью преобразования передаточной функции (4.4):

Здесь

есть Z-преобразование входной последовательности. Выходная последовательность получается с помощью соответствующего обратного преобразования (54). Функция A(z) называется цифровой передаточной функцией.

Теперь, используя выражение (4.4), можно непосредственно определить передаточную функцию цифрового фильтра, показанного на рис. 4.1. Из соотношения

получаем

Для определения частотной характеристики А(jw) подставим в формулу (4.8) , в результате получим:

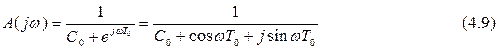
Функция является периодической с периодом 2pf₀. Это свойство — общее для всех цифровых фильтров. Для модуля частотной характеристики имеем:

График этой функции приведен на рис. 4.3. Видно, что эта амплитудно-частотная характеристика в области 0 £ wT₀ £ p, т.е. 0 £ f £ 1/2×f₀, имеет вид характеристики фильтра нижних частот как мы и ожидали, исходя из переходной характеристики на рис. 4.2.

На основании теоремы о дискретизация для дискретной системы задержки, работающей на частоте f₀, частота синусоидальной последовательности {x(t_i)} выбирается не больше чем 1/2×f₀,. В области частот f > 1/2×f₀ амплитудно-частотная характеристика устройства уже не имеет вида, присущего фильтру. Если все же желательно использовать такое устройство необходимо заменить цифровой элемент задержки аналоговым элементом задержки (например, линией задержки или фазовым фильтром).

4.2. Цифровая обработка сигналов

4.2.1. Реализация цифровых фильтров

Как мы видели в предыдущем разделе, с помощью цифрового фильтра входная последовательность {x(t_i)} может быть преобразована в выходную последовательность {y(t_i)} и при этом реализуется желаемая цифровая передаточная функция . Отсюда получается блок-схема, показанная на рис. 4.4. Для того чтобы выполнялись положения теоремы о дискретизации, ограничим полосу частот с помощью аналогового фильтра нижних частот. Посредством элемента выборки-хранения берутся выборки из ограниченного по полосе сигнала с интервалом T₀ = 1/f₀. Эти выборки с помощью аналого-цифрового преобразователя преобразуются в числовую последовательность {x(t_i)} и подаются на вход цифрового фильтра. Выходная последовательность {у(t_i)} может быть обработана далее в цифровой форме или с помощью цифро-аналогового преобразователя и фильтра нижних частот преобразована в непрерывный сигнал. При этом необходимо принять во внимание положения, изложенные в разд. 1.2.1. Дискретизация непрерывных сигналов по времени.

4.2.2. Представление сигналов и основные элементы

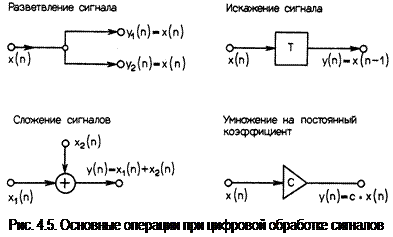
Функция цифровой фильтрации реализуется с использованием основных операций, схематически показанных на рис. 4.5:

· суммирование сигналов у(n) = х₁(n) + х₂(n);

· разветвление сигналов у₁(n) = у₂(п) = х(n); (4.10)

· умножение на постоянный коэффициент у(n) = С×х(n);

· задержка на один интервал дискретизации Т₀: у(n) = х(n - 1).

Все эти шаги обработки отсчетов х(n) совершаются во временной области. Для описания процессов преобразования в частотной области используется z-преобразование (обобщенное частотное представление, эквивалентное преобразованию Лапласа):

(4.11)

Тогда приведенные выше шаги преобразования можно записать в виде:

Y(z) = X₁(z) + Х₂(z) – суммирование сигналов;

Y₁(z) = Y₂(z) = Х(z) – разветвление сигналов;

Y(z) = C×X(z) – умножение на постоянный коэффициент;

Y(z) =X(z)×z^-1 – задержка сигнала.

Расчет частотной характеристики:

Для удобства расчетов аргумент z обычно заменяется выражением

(4.12)

где Т₀ = 1/f₀ – длительность интервала дискретизации. Далее составляется передаточная функция H(z} = Y(z)/X(z) и в нее подставляется выражение z, приведенное выше. Например, дифференциальное уравнение и передаточная функция для схемы на рис. 4.6, а (частный случай a₁=a₀) принимают вид:

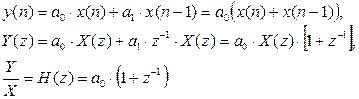
Введя сокращение 2pfТ₀=wT₀=Q и используя формулу Эйлера z=e^jQ= cos(Q) +j×sin(Q), получаем выражение для передаточной функции, состоящее из действительной и мнимой составляющих А и jB:

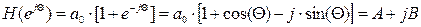
Модуль и фаза передаточной функции при а₁=a₀:

Теперь амплитудно-частотная и фазо-частотная характеристики выражаются в виде:

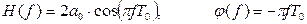
Видно, что фильтр является низкочастотным. Его амплитудно-частотная характеристика имеет косинусоидальную форму, а фазо-частотная характеристика линейна (фазо-линейными являются цифровые фильтры с симметричными переходными характеристиками; это условие удовлетворяется только в данном частном случае).

4.2.3. Структуры цифровых фильтров

Структуры цифровых нерекурсивных фильтров (FIR)

Основные структуры цифровых фильтров показаны на рис. 4.6. Нерекурсивный фильтр ("finite impulse response", FIR) – фильтр с однонаправленной цепью передачи («вперед»); его переходная характеристика h(n) имеет конечную длительность.

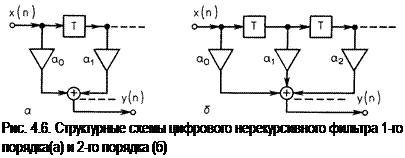Структуры цифровых рекурсивных фильтров (IIR)

Рекурсивный фильтр ("infinite impulse response", IIR)-фильтр, имеющий цепь обратной связи с выхода на вход; его переходная характеристика h(n) имеет бесконечную длительность.

Желательно, чтобы цифровые фильтры имели передаточную характеристику подобную характеристикам аналогового фильтра. Однако это невозможно, поскольку цифровой фильтр (как было показано в 4.1), в отличие от аналогового в диапазоне 0£f£¥ обладает периодической передаточной характеристикой. Однако у цифрового фильтра используемая полоса частот ограничена соотношением 0£f£f₀/2. Таким образом, можно потребовать, чтобы частотная характеристика ЦФ сохраняла желаемый вид (как передаточная характеристика аналогового фильтра) лишь до значения половины частоты дискретизации f₀/2.

Для этого можно модифицировать АЧХ аналогового фильтра посредством преобразования оси частот, таким образом, чтобы область 0£f£¥ отображалась в область 0£f£f₀/2 и на высоких частотах периодически повторялась (т.е. чтобы АЧХ аналогового фильтра стала похожа на АЧХ цифрового фильтра). Для этого введем вспомогательную переменную f’, такую чтобы соблюдается равенство:

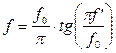(4.13)

При f®∞, как и требуется, f’®f₀/2. При f’<<f₀ имеем f≈f’. Следовательно, искажение частотной оси тем меньше, чем больше тактовая частота f₀ по сравнению с интересующим нас диапазоном частот. При синтезе аналоговых фильтров передаточная характеристика всегда представляется через нормированную частоту W=f/f_ср (где f_ср — характерная точка АЧХ аналогового фильтра, частота среза или резонансная частота). Для того, чтобы это нормированное представление можно было использовать для вычислений, введем нормированную частоту выборки

(4.14)

Используя выражение 4.13, получаем:

(4.15)

При таком преобразовании, конечно же, произойдет сдвиг характерной частоты фильтра (частоты резонанса, среза). Для того, чтобы эти частоты на логарифмической оси совпадали изменим множитель перед tg в формуле 4.15:

Из формулы 4.15 получаем:

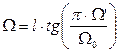, (4.16)

Где:

(4.17)

(4.18)

При этом W’=1 при W=1. Т.е. характерные частоты аналогового и цифрового фильтра совпадают. При этом интерпретируем формально введенную частоту W’ как новую переменную W и обозначаем преобразованную частотную характеристику через H’(jw). Очевидно, что полученная характеристика подобна характеристике аналогового фильтра.

Благодаря вышеописанным операциям преобразованная частотная характеристика H’(jw) имеет вид, позволяющий реализовать цифровой фильтр. Для расчета цифровой передаточной функции H_ц(w) теперь необходимо уравнение преобразования комплексной частотной переменной P. Подстановка P=jW (W=-Pj) в формулу 4.16 (4.18) дает:

Учитывая, что W₀=f₀/f_ср=1/(T₀×f_ср), 2pP’f_ср=p’ и , получаем:

(4.19)

Итак:

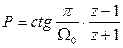(4.20)

Данное соотношение 4.20 называется билинейным преобразованием.

Таким образом, аналоговый фильтр можно преобразовать в цифровой следующим образом. В выражение для аналоговой передаточной функции H(Р) вместо нормированной комплексной частотной переменной Р подставляем переменную l×(z– 1)/(z+1) и получаем передаточную функцию H_ц (z), которая может быть реализована в цифровом фильтре. Амплитудно-частотная характеристика имеет в этом случае вид, подобный характеристике аналогового фильтра. Характеристика сжимается по частоте W таким образом, чтобы значение H(j¥) соответствовало частоте ¹/₂W₀. Появляющееся при этом ослабление тем меньше, чем больше W₀ по сравнению с представляющим интерес частотным диапазоном 0<W<W_max.

Фазово-частотная характеристика, естественно, изменяется сильнее. Следовательно, положения, относящиеся к аналоговой технике, нельзя переносить в область цифровых устройств. По этой причине, например, неразумно аппроксимировать амплитудно-частотную характеристику бесселевыми фильтрами, поскольку линейность фазы в этом случае нарушается. Такую задачу аппроксимации целесообразно решать непосредственно в z-области. При построении цифровых фильтров, как и для аналоговых фильтров, наиболее просто соединять блоки первого и второго порядка.

Расчет цифровых фильтров на заданную частотную характеристику проводится довольно просто с использованием билинейного преобразования. Для этого в передаточную функцию Н(P) аналогового фильтра вместо частотной переменной P подставляется ее выражение через переменную z:

Где f₀ – частота дискретизации, f_ср – частота среза или резонансная частота фильтра. В результате получается передаточная функция H_ц(z) цифровой системы. Так аналоговый фильтр n-го порядка преобразуется в рекурсивный цифровой фильтр того же порядка. Заметим при этом, что частотная характеристика аналогового фильтра в области 0 £ f_a £ ¥ неравномерно отображается при реализации соответствующего цифрового фильтра на область 0 £ f_ц £ f₀/2 (здесь f₀ – частота дискретизации), т.е. частотные характеристики аналогового и соответствующего ему цифрового фильтров оказываются различными, особенно в области верхних частот полосы пропускания. Если передаточная функция фильтра H_ц(z) определена, то реализовать ее можно с использованием разных схемных структур, которые, как и в случае аналоговых фильтров, будут обладать присущими им индивидуальными свойствами.

Свойства цифровых фильтров имеют свои пределы, связанные в основном с конечной длиной кодовых слов сигнала, выбором коэффициентов фильтра и элементами схемы, для которых ведется расчет (сумматор, умножитель, ЗУ). Наиболее характерные мешающие факторы:

· чувствительность к разбросу значений (конечная точность) коэффициентов фильтров;

· неустойчивость при перегрузках и малых уровнях сигнала рекурсивных фильтров;

· шумы округления в умножителях, обусловленные ограничением длины кодового слова результата.

Как можно видеть из всего сказанного выше, степень мешающего влияния указанных факторов можно уменьшить, если увеличить в доступных пределах длину кодовых слов внутри цифровой системы и правильно выбирать структуру схем.

Дата добавления: 2014-01-20