Уравнение неразрывности в интегральной форме

Система обучения

СО – всеобщая модель учебного процесса, соответствующая определенной методической концепции, которой обуславливаются отбор материала; цель, формы, содержание и средства обучения. СО – открытая, а не замкнутая система, поэтому внешние факторы влияют на нее и соответственно на весь процесс обучения ИЯ. Например, появляются новые технологии обучения, внедряются новейшие научные разработки.

На лекции № 2 была получена интегральная форма уравнения неразрывности:

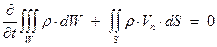(1)

где 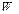- объём контрольного элемента, ограниченного поверхностью .

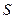Задача 1. Получить основное уравнение расхода несжимаемой жидкости в трубопроводе переменного сечения.

Решение: По условию задачи 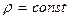и плотность можно вынести за знак интеграла. Тогда получим:

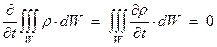(2)

Уравнение неразрывности принимает вид:

,

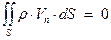Или

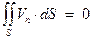(3)

где 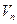- нормальная составляющая скорости к поверхности .

Рассмотрим трубопровод переменного сечения:

Выделим пунктиром контрольный элемент W и контрольную поверхность 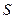. Разобъём контрольную поверхность на три области: область 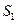- поперечное сечение на входе жидкости в трубопровод, - поперечное сечение на выходе жидкости из трубопровода, - боковая поверхность трубопровода.

Уравнение (3) можно представить как сумму трёх интегралов:

(4)

Знак минус перед первым интегралом поставлен потому, что направление скорости 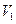и нормали к области противоположны. В уравнении (4) последнее слагаемое равно нулю, так как скорость равно нулю (стенки трубопровода непроницаемы). В отношении двух других интегралов воспользуемся теоремой о среднем значении интеграла и получим алгебраическое равенство:

или (5)

Ответ: 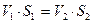(6)

В уравнении (6) скорост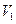и и 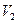есть средние значения скоростей в сечениях 1 и 2, площади которых обозначены соответственно 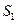и

Задача 2. Получить основное уравнение расхода жидкости в трубопроводе переменного сечения в условиях установившегося режима течения.

Ответ: (7)

Задача 3. (John J.E. Introduction to fluid mechanics. N.Y.,1980. p.587)

В установившемся режиме работы насоса распределение скорости жидкости во всасывающем патрубке (сечение 1-1) имеет параболический вид:

,

а на выходе из насоса (сечение 2-2) – равномерное распределение скорости: .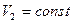

Найти скорость 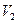, если

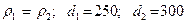(диаметры указаны в мм, скорость – м/с)

Решение.

Для установившегося режима течения жидкости справедливо:

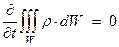
Выберем контрольную поверхность, как показано пунктиром на рисунке. Стенки патрубков и насоса непроницаемы, следовательно, 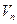на боковых поверхностях равна 0. Из уравнения неразрывности получаем:

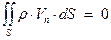
(8)

Раскроем подинтегральные выражения и используем равенство

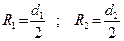, где (9)

Выполним интегрирование:

(10)

Отсюда получаем:

Задача 4. В установившемся режиме работы насоса распределение скорости жидкости во всасывающем патрубке имеет вид:

,

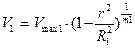а распределение скорости на выходе из насоса имеет вид

Известно: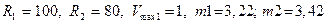

Найти максимальную скорость на выходе из насоса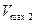

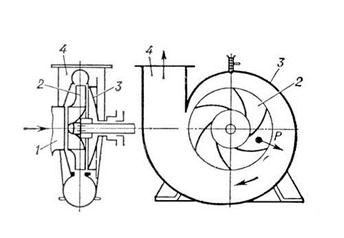
Схема центробежного насоса с односторонним подводом жидкости на рабочее колесо: 1 — отверстие для подвода жидкости; 2 — рабочее колесо; 3 — корпус; 4 — патрубок для отвода жидкости

(продолжение следует)

Дата добавления: 2014-01-20