Асимптоты. Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении этой точки от начала

Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении этой точки от начала координат.

Асимптоты могут быть вертикальными, наклонными и горизонтальными.

Вертикальные асимптоты.

Прямая является вертикальной асимптотой графика функции 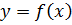, если

Обычно такими точками являются точки разрыва второго рода (рис. 77). Для отыскания вертикальных асимптот нужно найти те значения 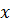, вблизи которых функция неограниченно возрастает по модулю. Так функция обратной пропорциональности имеет вертикальную асимптоту 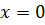, т. е. ось (рис. 78).

Наклонные и горизонтальные асимптоты.

Уравнение наклонной асимптоты имеет вид 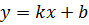. Пусть - произвольная точка графика функции 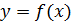, по формуле расстояния от точки до прямой, имеем
Так как

Разхделим обе части равенства на 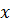, получим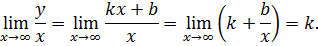

Применяя к левой части правило Лопиталя, получим

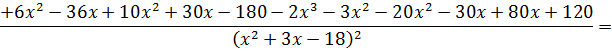
Отсюда

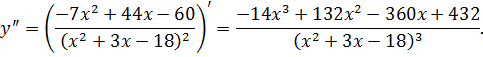
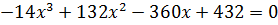Отсюда и или

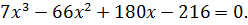Проверяя целые делители числа 216, убеждаемся, что значение 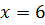является корнем уравнения. Разделив в соответствии с теоремой Безу выражение в правой части на 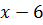, получим разложение на множители

Уравнение корней не имеет, так как дискриминант

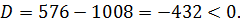
Нанесем на числовую ось точки, в которых вторая производная равна нулю или не существует и определим промежутки выпуклости и вогнутости.

Из рисунка видно, что вторая производная функции положительна на промежутках и 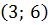, следовательно, на них график является выпуклым. На промежутках и 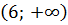вторая производная отрицательна и функция является выпуклой на них. В точке 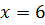функция определена и меняет знак с (+) на (-) и поэтому она является точкой перегиба, причем

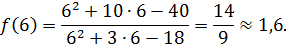
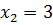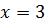6) Исследуем график на асимптоты. Так как функция в точках и имеет разрыв второго рода, то прямые и являются вертикальными асимптотами. Для определения наклонных (и горизонтальных) асимптот вида 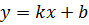, определим коэффициенты 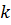и .

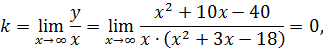
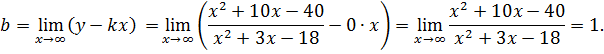
Таким образом график функции имеет горизонтальную асимптоту .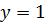

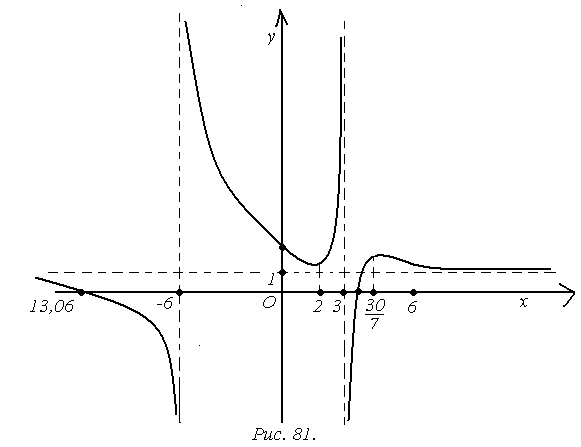
На основании полученных данных, строим график функции (рис. 81).

Дата добавления: 2014-01-20