Колебания в биологических объектах

Таким образом, колебания охватывают огромную область физических явлений и технических процессов.

Классификация колебаний по характеру взаимодействия с окружающей средой:

свободные (или собственные) — это колебания в системе под действием внутренних сил, после того как система выведена из состояния равновесия (в реальных условиях свободные колебания почти всегда затухающие).

Например, колебания груза на пружине, маятника, моста, корабля на волне, струны; колебания плазмы, плотности и давления воздуха при распространении в нём упругих (акустических) волн.

Чтобы свободные колебания были гармоническими, необходимо, чтобы колебательная система была линейной (описывалась линейными уравнениями движения), и в ней отсутствовала диссипация энергии (последняя вызвает затухание).

вынужденные — колебания, протекающие в системе под влиянием внешнего периодического воздействия. При вынужденных колебаниях может возникнуть явление резонанса: резкое возрастание амплитуды колебаний при совпадении собственной частоты осциллятора и частоты внешнего воздействия.

автоколебания — колебания, при которых система имеет запас потенциальной энергии, расходующейся на совершение колебаний (пример такой системы — механические часы). Характерным отличием автоколебаний от свободных колебаний является, то, что их амплитуда определяется свойствами самой системы, а не начальными условиями.

параметрические — колебания, возникающие при изменении какого-либо параметра колебательной системы в результате внешнего воздействия,

случайные — колебания, при которых внешняя или параметрическая нагрузка является случайным процессом,

связанные колебания - свободные колебания взаимно связанных систем, состоящих из взаимодействующих одиночных колебательных систем. Связанные колебания имеют сложный вид вследствие того, что колебания в одной системе влияют через связь (в общем случае диссипативную и нелинейную) на колебания в другой

колебания в структурах с распределенными параметрами (длинные линии, резонаторы),

флуктуационные, происходящие в результате теплового движения вещества.

.

Условия возникновения колебаний.

1. Для возникновения колебания в системе необходимо вывести её из положения равновесия. Например, для маятника сообщив ему кинетическую (удар, толчок), либо – потенциальную (отклонение тела) энергию.

2. При выведении тела из положения устойчивого равновесия возникает равнодействующая сила, направленная к положению равновесия.

С энергетической точки зрения это значит, что возникают условия для постоянного перехода (кинетической энергии в потенциальную, энергии электрического поля в энергию магнитного поля и обратно.

3. Потери энергии системы за счет перехода в другие виды энергии (часто в тепловую энергию) малы.

Характеристики колебательного процесса.

На рис.1 представлен график периодического изменения функции F(x), которое характеризуется параметрами:

Амплитуда — максимальное отклонение колеблющейся величины от некоторого усреднённого её значения для системы.

Период — наименьший промежуток времени, через который повторяются какие-либо показатели состояния системы (система совершает одно полное колебание), T (c).

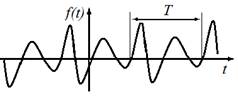
Рис.1.1. Периодическая функция времени

Частота — число колебаний в единицу времени, f (Гц, с⁻¹), ( в оптике принято частоту обозначать символом 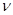(Гц, с⁻¹)).

Период колебаний T и частота f — обратные величины:

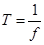и .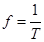

В круговых или циклических процессах вместо характеристики «частота» обычно используется понятие круговая (циклическая) частота.

Круговая (циклическая) частота 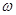(рад/с, Гц, с⁻¹), показывает число колебаний за 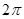единиц времени:

.

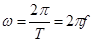К этой величине следует относиться как к удобной вспомогательной математической величине

Фаза колебаний определяет состояние колебательной системы в любой момент времени. Измеряется в радианах (рад).

Фаза колебания в начальный момент времени (t=0) называется начальной фазой (j₀).

Гармонические колебания.

Гармоническое колебание — это колебание, при котором физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний может быть представлено в виде:

,

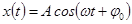где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд 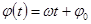— полная фаза колебаний, 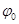— начальная фаза колебаний. Гармоническое колебание может рассматриваться как проекция вектора амплитудой А, при его вращении с угловой скоростью ω (рис.2).

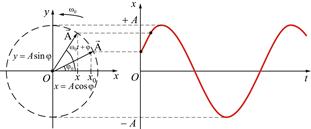
Рис. 1.2. Эволюция во времени смещения x при гармоническом движении.

Мгновенная скорость является первой производной координаты по времени, поэтому функция скорости является первой производной от функции смещения 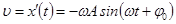. Величина 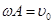равна максимальной скорости движения точки при гармонических колебаниях. Отметим, что при гармонических колебаниях скорость точки также изменяется по гармоническому закону. Аналогично зависимость ускорения от времени является первой  производной от скорости или второй производной координаты (3)

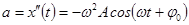
На рис. показаны графики зависимостей координаты , скорости 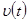и ускорения 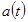точки, совершающей гармонические колебания. Все эти зависимости описываются гармоническими функциями одного периода (одинаковой частоты), сдвинутыми друг относительно друга на четверть периода, (которой соответствует сдвиг фазы на 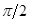. Между нулями и экстремумами этих функций существуют очевидные соответствия: координата движущейся точки достигает максимального и минимального значения, когда ее скорость обращается в нуль; модуль скорости максимален, когда точка проходит через нулевую координату; модуль ускорения максимален, когда скорость равна нулю, а отклонение точки максимально. Отметим, что ускорение при колебательном процессе всегда противоположно по знаку смещению: .

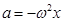 При гармонических колебаниях ускорение точки пропорционально его координате, с отрицательным коэффициентом пропорциональности.

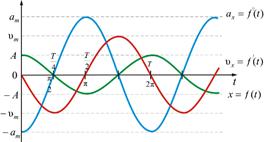
Рис.1. 3. Эволюция во времени перемещения x, скорости v и ускорения a при гармоническом движении.

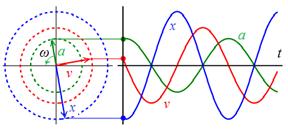
Рис. 1.4. Векторное представление и эволюция во времени перемещения x, скорости v и ускорения a при гармоническом движении.

Важное свойство гармонических колебаний: период и частота этих колебаний не зависят от их амплитуды. Амплитуда колебаний определяется начальными условиями, то их частота полностью определяется параметрами колебательной системы (собственные колебания)и внешним воздействием (вынужденные колебания). Гармонические колебания возникают в физических системах различной природы, описываемых дифференциальными уравнениями: .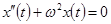

Гармонические колебания выделяются из всех остальных видов колебаний по следующим причинам:

• Очень часто^[2] колебания с малой амплитудой, как свободные, так и вынужденные, которые происходят в реальных системах, имеют форму гармонических колебаний или очень близкую к ним.
• Широкий класс периодических функций может быть разложен на сумму тригонометрических компонентов с кратными частотами (разложение Фурье). Другими словами, любое колебание может быть представлено как сумма гармонических колебаний (см.лекцию 3).
• Для широкого класса систем откликом на гармоническое воздействие является также гармоническое колебание (свойство линейности), при этом связь воздействия и отклика является устойчивой характеристикой системы. Это позволяет исследование прохождения колебаний произвольной формы через системы свести к решению систем алгебраических уравнений.

Не все колебания являются гармоническими, однако этот тип колебаний является простейшей моделью колебательного движения достаточно часто встречающегося в действительности

Псевдогармоническое колебание — разновидность колебаний, для которых возвращающая сила (сила, стремящаяся вернуть тело в равновесное состояние) не является линейной по величине отклонения Общий вид дифференциальных уравнений описывающих псевдогармонические колебания имеет вид:

.

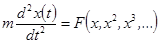Если можно пренебречь всеми членами F нелинейными по x, то данное уравнение переходит в уравнение гармонических колебаний.

Способы представления колебательных движений:

1. Аналитическое.

Дата добавления: 2014-01-20