Двойной интеграл в декартовых координатах

Предположим, что область 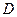, на которой определен двойной интеграл 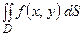, задана неравенствами

.

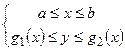Разобьем эту область на части 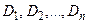прямыми, параллельными координатным осям. Будем считать, что каждая из этих прямых пересекает область не более чем в двух точках (рис. 2). В противном случае область следует разбить на несколько областей.

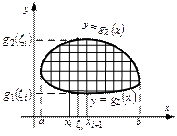
Рис. 2.

При таком способе дробления площадь каждой частичной области равна , где 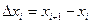, 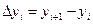. Двойной интеграл как предел интегральной суммы можно записать в виде:

,

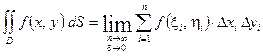где ранг дробления .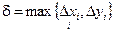

Зафиксируем значение 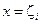и запишем интегральную сумму в виде:

.

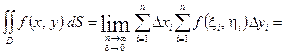
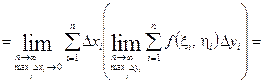
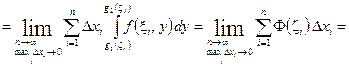
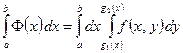Аналогично можно показать, что если область 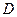, на которой определен двойной интеграл 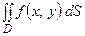, задана неравенствами

,

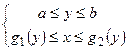то двойной интеграл по этой области можно представить в виде

.

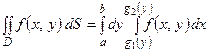Дата добавления: 2014-01-20