Вероятностная неопределенность

Предположим, что у агента появилась дополнительная информация о значении неопределенного параметра q, принадлежащего множеству W. Допустим, агенту известно распределение вероятностей на этом множестве (соответствующая неопределенность называется вероятностной), тогда логично использовать это знание, и устранять неопределенность следующим образом: у агента есть целевая функция f (×), зависящая от его действия и значения неопределенного параметра. Давайте возьмем от нее математическое ожидание по известному распределению, получим функцию ожидаемой полезности («ожидаемой» с точки зрения математического ожидания) 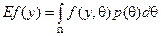. Таким образом, устранив неопределенность взятием математического ожидания, снова получили детерминированную модель (в выражение (2) раздела 2.1.1 можно вместо f (y) подставить E f (y)) и теперь можно максимизировать функцию ожидаемой полезности, зависящей только от действия агента, выбором этого действия.

Возможны и другие способы устранения неопределенности. Можно рассчитать риск, например, вероятность того, что значение целевой функции окажется меньше, чем заданное. И этот риск минимизировать, т.е. использовать не первый момент распределения, а дисперсию и другие характеристики. Подходы могут быть разными, но, главное – устранить зависимость от неопределенного параметра (что необходимо в силу гипотезы детерминизма), а потом принимать решения в условиях полной информированности.

Пример 2.5. Усложним Пример 2.1, а именно, предположим, что агент полагает, что рыночная цена l описывается вероятностным распределением p (l). Обозначим E l = – математическое ожидание цены. В силу линейности целевой функции (3) раздела 2.1.1 по цене, получаем, что E f (y) = (E l) y – y ² / 2 r. Действием агента, максимизирующим его ожидаемую полезность, будет y^* = min{(E l) r, y⁺ }. ·

Отношения предпочтения. Неопределенность может присутствовать и в моделях предпочтений, описываемых бинарными отношениями. Приведем пример.

Пример 2.6. Усложним Пример 2.3 c фирмой, выходящей на рынок, а именно, предположим, что результат z действия y зависит не только от самого действия ЛПР, но и от некоторых внешних по отношению к ЛПР факторов, то есть зависимость результата от действия имеет вид z = w(y, q, u), где q и u – факторы, не зависящие от ЛПР. Множества возможных значений этих параметров обозначим W и U соответственно. Если эти факторы известны на момент принятия решения, задача сводится к детерминированному случаю. Если же они неизвестны, возникает неопределенность.

Так, множество W может быть совокупностью объективных рыночных факторов. Например, состояние q ₁ = «новая продукция фирмы найдет спрос» приводит к высоким прибылям (исход z ₃), а состояние q ₂ = «новая продукция не найдет спроса» – к исходу «разорение» (z ₀). Множество U описывает неопределенность действий других лиц и может иметь, например, вид: { u ₁, u ₂}, где вариант u ₁ соответствует тому, что конкуренты предпримут активные действия по вытеснению фирмы с традиционного рынка, а вариант u ₂ – их пассивному поведению по поводу нового конкурента. Будем считать, что в первом случае фирма сможет получать лишь низкие прибыли (исход z ₁), а во втором – средние (z ₂).

Теперь уже выбор ЛПР некоторого действия y^* не приводит к единственному возможному результату. В зависимости от реализации не зависящих от ЛПР факторов q и u может реализоваться любой результат из множества R (y^*) = { w (y^*,q, u) | q Î W, u Î U }. Чтобы сделать выбор, ЛПР необходимо научиться сравнивать эти множества. Однако отношение предпочтения на системе множеств R (×) не задано условиями задачи. Его необходимо получать (возможно, используя некоторые дополнительные предположения) из отношения предпочтения на множестве результатов A ₀.

Так, если известно распределение вероятностей реализации событий из W и U, то можно определить вероятности появления различных результатов при выборе определенного действия.

Например, пусть P (q ₁) = 80 %, P (q ₂) = 20 % (то есть шансы того, что новая продукция найдет спрос – четыре к одному), и, кроме того, P (u ₁) = 50 %, P (u ₂) = 50 % (то есть различное отношение к новому конкуренту на традиционном рынке равновероятно).

Тогда, если фирма выходит на новый рынок (выбирает действие y ₁), то:

P (z ₃| y ₁) = 80%.

P (z ₀| y ₁) = 20%.

Соответственно, для других действий вероятности различных исходов будут следующими:

P (z ₁| y ₂) = 50%.

P (z ₂| y ₂) = 50%.

P (z ₁| y ₃) = 100%.

Остальные исходы имеют нулевую вероятность.

В соответствии с терминологией, введенной выше, описанная задача – это задача принятия решения в условиях вероятностной неопределенности.

Немногим отличается случай, когда ЛПР не имеет информации о вероятностях некоторых значимых событий, но имеет предположения о них. В этом случае объективные вероятности заменяются субъективными, и реализуется та же схема решения.

Таким образом, в данном примере каждое решение (действие) ЛПР приводит к лотерее, случайному процессу, в котором исходы могут реализовываться с некоторыми вероятностями. Для того, чтобы от предпочтения на множестве исходов перейти к предпочтениям на множестве действий, ЛПР должен уметь сравнивать свои предпочтения на множестве подобных лотерей, то есть определять, какая из лотерей для него лучше или хуже. Тогда оптимальным решением будет действие, приводящее к наилучшей лотерее.

Дата добавления: 2014-01-20