Определение 1

Игрой n лиц в нормальной форме называется совокупность

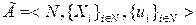, (1)

Содержащая для каждого игрока :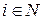

– множество стратегий 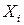, элементы которого (возможные действия игрока 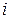) обозначаются ;

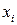– функцию выигрыша (функцию полезности, целевую функцию, критерий оптимальности) 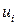, являющуюся отображением из 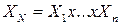в 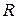. Элемент 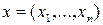множества 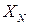называется исходом (ситуацией) игры (1).

Каждый игрок 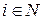выбирает любую стратегию 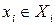. После того, как все игроки выбрали свои стратегии, определяется исход 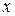и выигрыш каждого игрока 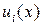при этом исходе. Таким образом, выигрыш каждого игрока зависит в общем случае от действий всех остальных игроков.

Предположим, что игроки в игре (1) действуют изолированно, т.е. каждый игрок выбирает свою стратегию независимо от того, какие стратегии выбирают другие участники. Игроки не обмениваются информацией. На выбор игроков не оказывает влияния прошлое.

Будем пока считать, что каждому игроку известна только его собственная функция выигрыша; функций выигрыша остальных игроков он может не знать.

Дата добавления: 2014-01-20