Лемма 2

Определение 5.

Стратегии i-го игрока 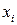и 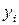называются эквивалентными, если они не различимы с его точки зрения:

.

Пусть в игре (1) множество недоминируемых стратегий i-го игрока не пусто: 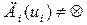, множества стратегий 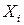компактны, функции выигрыша 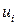непрерывны, .

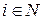Тогда следующие утверждения эквивалентны:

– существует доминирующая стратегия i-го игрока: ;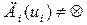

– все стратегии в множестве эквивалентны.

…..если у игрока есть хотя бы одна доминирующая стратегия, то все доминирующие стратегии эквивалентны и совпадают с его недоминируемыми стратегиями. В этом случае будем считать, что если игрок использует одну из них (при некооперативном поведении, то есть действуя изолированно от других игроков). С другой стороны, если у i-го игрока нет доминирующей стратегии (наиболее частый случай), то его недоминируемые стратегии неэквивалентны, поэтому его некооперативное поведение не может быть определенно однозначно. Требуется дополнительные предположения об информации, которой располагают игроки (в частности, о функциях выигрыша).

Равновесие в доминирующих стратегиях постулируется рациональным некооперативным поведением изолированных игроков.

Пример 1: «дилемма заключенного».

Каждый из двух игроков располагает двумя стратегиями А и Р, где А обозначает агрессивность, Р – миролюбие. Предположим, что «мир» (оба игрока миролюбивы) лучше для обоих игроков, чем «война» (оба игрока агрессивны), но односторонняя агрессия (один игрок агрессивный, а другой миролюбивый) выгоднее агрессорам. Типичная структура выигрышей имеет следующий вид:

Р1
А1
Р2	А2

Стратегиями первого игрока являются строки платежной матрицы: а стратегиями второго игрока – столбцы 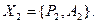результаты игры приведены в матрице 2х2, причем «северо-западное» число обозначает выигрыш первого игрока, а «юго-восточное» - выигрыш второго игрока, например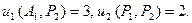

Очевидно, для обоих игроков стратегия А доминирует стратегию Р. Таким образом, единственное равновесие в доминирующих стратегиях имеет вид 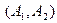, т.е. постулируется, что результатом некооперативного поведения является война. В то же время исход 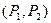(мир) дает больший выигрыш сразу обоим игрокам.

Таким образом, некооперативное эгоистическое рациональное поведение вступает в противоречие с коллективными интересами, которые в данном случае диктует выбор мирных стратегий. В то же время, если игроки не обмениваются информацией, то война является наиболее вероятным исходом; изолированность стратегических выборов может нанести определенный ущерб общественным интересам.

Определение Исход 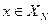в игре (1) доминирует по Парето исход , если

Исход х называется оптимальным по Парето, если он не доминирует по Парето.

Пример 2: «услуга за услугу».

Если у одного участника есть несколько доминирующих стратегий, то для него они эквивалентны, но, возможно, неэквивалентны для остальных. Рассмотрим следующую игру двух лиц, в которой стратегии каждого участника влияют только на выигрыш другого, но не на свой собственный:

благожелательность к игроку 2
неблагожелательность к игроку 2
	благожелательность к игроку 1	неблагожелательность к игроку 1

Любой исход является равновесием в доминирующих стратегиях (проверьте!), но только один из них (благожелательность к игроку 2, благожелательность к игроку 1) оптимален по Парето.

Если у 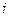-го игрока не имеется информации о функциях выигрыша остальных игроков, то он не может исключать из рассмотрения какие-либо допустимые стратегии их .

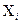Один из способов исключения стратегий на множестве состоит в удалении доминируемых стратегий. Другой путь соответствует пессимистическому предположению (исключающему риск), что случиться худшее.

Определение 7. В игре (9.1) стратегия является осторожной стратегией -го игрока, если

Обозначим через 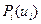множество осторожных стратегий -го игрока. Осторожное поведение практически реализуемо и совместимо с правилом исключения доминирующих стратегий. Именно, справедлив следующий результат.

Лемма 3. Пусть множества 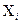компактны, а функции 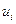непрерывны для всех 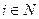. Тогда множество 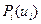осторожных стратегий не пусто, компактно и пересекается с множеством недоминируемых стратегий:

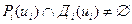
Используя осторожную стратегию, игрок гарантирует себе выигрыш 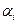, который называется гарантированным выигрышем. Если набор 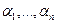гарантированных выигрышей оптимален по Парето, то осторожные стратегии также могут быть названы оптимальными.

Определение 8. Игра в нормальной форме (1) несущественна, если нет исхода , для которого

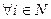
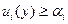
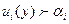
В несущественной игре осторожные стратегии оптимальны в следующем смысле.

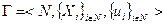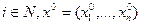Теорема 1. Пусть игра несущественна, - осторожная стратегия игрока для всех . Тогда:

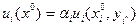
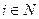1. для всех и ;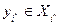

2. 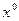– оптимальный по Парето исход;

3. для любого подмножества 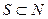и любого набора стратегий 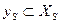одновременное выполнение следующих двух условий невозможно:

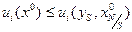
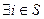
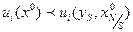
Доказательство. Поскольку 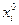- осторожная стратегия -го игрока, то

Поскольку игра несущественна, то 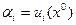для всех и утверждение 1 теоремы доказано.

Утверждение 2 следует из 3 при 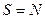. Для доказательства утверждения 3 выберем и 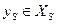такие, что

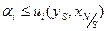(9.2)

Применяя утверждение 1 к 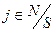, получаем

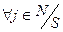
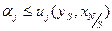
Объединяя обе системы неравенств для всех и учитывая несущественность игры, получаем 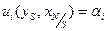. Следовательно, строгое неравенство в (9.2) невозможно.

Согласно утверждению 1, если игрок использует оптимальную (т.е. осторожную) стратегию и ожидает, что остальные сделают то же самое, то он получит гарантированный выигрыш 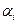. Если некоторые игроки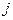 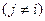откажутся от использования оптимальных стратегий, то это может быть только выгодно игроку .

Свойство 3 означает, что никакой отдельный игрок и никакая коалиция (подмножество) игроков не имеют причин для одностороннего отхода от оптимальных стратегий.

Заметим, что в игре, которая не является несущественной, никакой набор стратегий 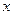не может быть назван оптимальным. В самом деле, два требования оптимальности суть для всех и оптимальность исхода по Парето. По определению 8 эти условия вместе приводят к тому, что для некоторого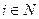

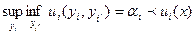
Иначе говоря, игрок не может гарантировать себе выигрыш 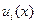и может подвергнуться угрозам со стороны дополнительной коалиции .

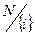Определение 9: Стратегия называется доминантной стратегией игрока i, если для любой обстановки 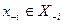и для любых 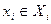справедливо неравенство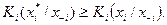

Это определение означает, что, если у игрока, независимо от действий противников, есть стратегия, дающая ему максимальный по сравнению с другими его стратегиями выигрыш, то эта стратегия называется доминантной.

Целесообразность использования каждым игроком своих доминантных стратегий очевидна.

Определение 10: Если для каждого игрока i существует доминантная стратегия ,то исход 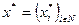называется равновесием в доминантных стратегиях (РДС).

Равновесие в доминантных стратегиях существует далеко не для всех игр. Приведем несколько лемм, определяющих некоторые классы игр, в которых существует равновесие в доминантных стратегиях.

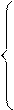Лемма 2. Если в игре n лиц 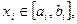функции выигрыша непрерывны по совокупности стратегий и для каждого игрока частная производная 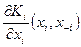существует и везде знакопостоянна, то существует РДС. При этом доминантной стратегия , i-гоигрока будет стратегия

=

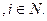
Идею леммы 2 можно обобщить на значительно более широкий класс игр.

Лемма 3. Если в игре п лиц 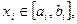а функция выигрыша произвольного игрока i сепарабельна по стратегии этого игрока, то есть 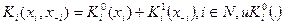имеет единственный максимум на множестве действий 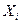то существует РДС, причем для игрока i его доминантная стратегия:

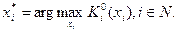
Для доказательства лемм 2 и 3 достаточно проверить определение РДС.

Равновесие Нэша. Гораздо чаще, чем РДС, существует равновесие Нэша (РН). Джон Нэш, американский математик, в начале 50-х годов XX века предложил следующее: устойчивым исходом взаимодействия агентов можно считать такой вектор их действий, от которого в одиночку никому из них не выгодно отклоняться. Это значит, что ни один из агентов, в одиночку меняя свою стратегию на другую, не может увеличить свой выигрыш при условии, что остальные своих стратегий не меняют.

Формальное определение равновесия Нэша 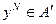таково:

(5) ,

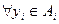
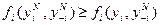то есть для любого агента и для любого допустимого его действия выбор им равновесного по Нэшу действия дает ему выигрыш не меньший, чем при выборе любого другого действия при условии, что остальные игроки играют равновесные по Нэшу стратегии.

Отличие между изложенными подходами (РДС и равновесием Нэша) заключается в том, что в формулировке равновесия в доминантных стратегиях (3) фигурирует произвольная обстановка, то есть доминантная стратегия – наилучшая при любой обстановке. А стратегия по Нэшу – наилучшая при «нэшевской» обстановке (см. (5)).

Равновесие Нэша хорошо тем, что в большинстве моделей оно существует. Одним из его недостатков является то, что оно не всегда единственно. Ведь если есть два равновесия, то как предсказать, в каком из них окажутся агенты. Нужны дополнительные предположения.

Кроме того, равновесие по Нэшу не устойчиво к отклонению двух и более игроков. По определению одному агенту не выгодно отклоняться, но это не значит, что если два агента договорились и одновременно отклонились от равновесной ситуации, то они не смогут оба выиграть. То есть равновесие Нэша – существенно некооперативная концепция равновесия.

Дата добавления: 2014-01-20