Действия над комплексными числами

1. Сложение.

Дано:

z1 = x1 + iy1;

z2 = x2 + iy2;

z1 + z2 = x1 + iy1 + x2 + iy2 = (x1+ x2) + i·(y1+ y2);

Пример: z1 = 3 – 2i

z2 = -4 + 5i;

z1 + z2 = -1 + 3i; z1 – z2 = 7 + i (-7) = 7 – 7i;

2.1.Умножение.

Дано:

z1 = x1 + iy1;

z2 = x2 + iy2;

z1 · z2 = (x1 + iy1) · (x2 + iy2) = x1· x2 + iy1·x2 + iy2·x1 + i2 y1·y2 = (x1· x2 – y1·y2) +

= -1

+ i·(x1·y2 + x2·y1).

Пример:

(3+i)(-4 – 3i) = -12 – 4i – 9i – 3 i2 = -9 –13i;

2.2. Умножение комплексных чисел в тригонометрической форме.

Пусть комплексные числа даны в тригонометрической форме:

z1 = ρ1·(cos(φ1) + i·sin(φ1));

z2 = ρ2·(cos(φ2) + i·sin(φ2)); тогда

z1·z2 = ρ1·ρ2 · (cos(φ1) + i·sin(φ1)) · (cos(φ2) + i·sin(φ2)) = ρ1·ρ2 · [(cosφ1·cosφ2 –

– sinφ1 · sinφ2) + i· (cosφ1·sinφ2 + sinφ1·cosφ2)] = ρ1·ρ2 · (cos(φ1+φ2) + i· sin(φ1+φ2))

Вывод: при умножении комплексных чисел в тригонометрической форме модули перемножаются, а аргументы складываются (пример см.выше).

3.Деление.

Дано:

z1 = x1 + iy1;

z2 = x2 + iy2;

z1 = x1 + iy1 = (x1 + iy1)(x2 – iy2) = (x1· x2 + y1·y2) + i·(x2·y1– x1·y2) = x1·x2 +y1·y2 +

z2 x2 + iy2 x22 – iy22 x22 + y22 x22 + y22

+ i· (x2·y1– x1·y2);

x22 + y22

Пример: z1 = (1–i)(4 – 2i) = (4-2) + i(-4-2) = 2 – 6i = 1 – 3 i.

z2 (4+2i)(4– 2i) 16 – 4i2 20 10 10

3.2. Деление комплексных чисел в тригонометрической форме.

z1 = ρ1·(cos(φ1) + i·sin(φ1)) = ρ1 · (cos(φ1) + i·sin(φ1)) ·(cos(φ2) – i·sin(φ2)) =

z2 ρ2·(cos(φ2) + i·sin(φ2)) ρ2 cos2(φ2) + sin2(φ2)

= ρ1 · [cos(φ2) ·cos(φ1) + sin(φ2) ·sin(φ1)) + i·(sin(φ1) ·cos(φ2) – cos(φ1) ·sin(φ2)] =

ρ2

= ρ1 · (cos(φ1–φ2) + i· sin(φ1–φ2)).

ρ2

вывод: при делении комплексного числа модули делятся, а аргументы вычитаются.

Пример: z1= 2(cos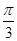+ i·sin)

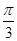z1= 3(cos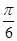+ i·sin)

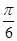z1 · z2 = 2 · 3 (cos(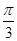+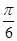) + i·sin(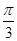+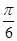) = 6 (cos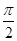+ i·sin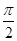) = 0+6i = 6i;

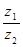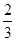= · (cos(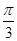–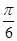) + i·sin(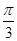–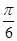) = 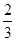·(cos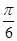+ i·sin) = ;

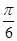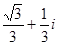4. Возведение в степень комплексного числа.

zn = z · z · z ·… · z;

n раз

z = ρ·(cos(φ) + i·sin(φ)), на основании умножения комплексных чисел в тригонометрической форме имеем:

zn = ρ· ρ· ρ… ρ · (cos(φ + φ + φ …+ φ) + i·sin(φ + φ + φ …+ φ))

n раз n раз n раз

zn = ρn·(cos(φ) + i·sin(φ)).

Пример: z = 1+·i; z5 -?

x =1;

x = ;

ρ = 2; tg(φ)= ; φ = ;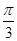

z = ρ·(cos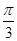+ i·sin)

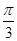z5 = 25·(cos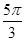+ i·sin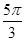) = 32 ·(cos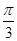– i·sin).

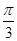5. Извлечение корня n-ой степени из комплексного числа ω, если выполняется соотношение zn = ω и обозначается z = ;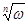

Пусть данное ω = r·(cosθ + i · sinθ), искомое k число

z = ρ·(cos(φ) + i·sin(φ)), тогда соотношение zn = ω перепишется в виде:

ρn·(cos(φ) + i·sin(φ)) = r·(cosθ + i · sinθ);

ρn = r;

ρ = 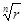; nφ = θ + 2πk;

φ = ;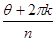

z = 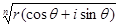= 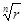· (cos(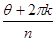) + i·sin());

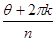Пример: Найти z == ;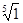

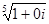1 + 0·i = 1 (cos0 + i·sin0), тогда

z = 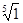(cos (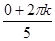) + i·sin(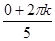)) = (cos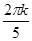+ i·sin);

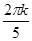давая значения k = 0,1,2…,n-1 получаем n корней;

в данном случае k = 0,1,2,3,4.

k = 0, z =1;

k = 1, z =1(cos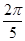+ i·sin);

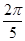k = 2, z =1(cos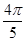+ i·sin);

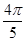k = 3, z =1(cos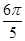+ i·sin);

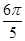k = 4, z =1(cos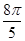+ i·sin).

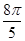Дата добавления: 2014-01-20