Теорема Гаусса

Рассмотрим поле точечного заряда 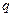и вычислим поток вектора напряженности 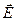через замкнутую поверхность 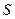, заключающую в себе заряд (рис. 6.1). Поток вектора 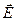через любую замкнутую поверхность равен числу линий, входящих наружу, т.е. начинающихся на заряде, если он положителен, и числу линий, входящих внутрь, т.е. оканчивающих на точечном заряде, если он отрицателен. Учтя, что количество начинающихся или оканчивающихся на точечном заряде лини численно равно 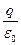, можно написать, что

. (6.1)

Знак потока совпадает со знаком заряда.

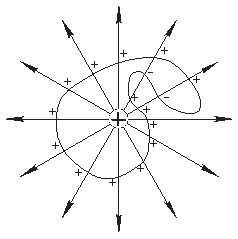Рис. 6.1

Теперь допустим, что внутри замкнутой поверхности находятся 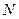точечных зарядов . В силу принципа суперпозиции напряженность 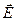поля, создаваемого всеми зарядами, равна сумме напряженностей 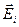, создаваемых каждым зарядом в отдельности: 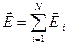. Поэтому

.

Каждый из интегралов, стоящих под знаком суммы, равен 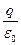. Следовательно,

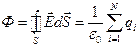. (6.2)

Данное утверждение носит название теоремы Гаусса: поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на .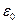

Заряды в пространстве могут распределяться не только дискретно, но и непрерывно. В этом случае вводится понятие о плотности зарядов. При непрерывном распределении зарядов по поверхности вводят поверхностную плотность заряда. Пусть заряд 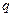равномерно распределён по поверхности площадью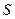. Тогда поверхностной плотностью заряда 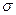называется отношение 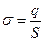. Если же распределение заряда неравномерное, то надо выделить на поверхности элементарный участок 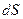, в пределах которого заряд , находящийся на нём, можно считать равномерно распределённым. Тогда поверхностная плотность заряда будет равна:

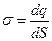, (6.3)

т.е. поверхностной плотностью зарядов называется заряд, приходящийся на единицу площади. Из (6.3) следует 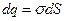и заряд 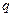на некоторой поверхности 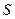равен интегралу , где интегрирование происходит по всей поверхности. С учетом вышесказанного теорема Гаусса для поверхностно распределенного заряда принимает вид:

. (6.4)

Аналогично вводится понятие объёмной плотности электрических зарядов. Объёмная плотность заряда 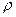находится по формуле:

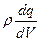, (6.5)

т.е. объёмная плотность зарядов равна заряду, приходящемуся на единицу объёма. Используя (6.5), можно найти заряд, расположенный в некотором объёме V: 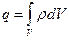, здесь интегрирование производится по всему объёму V, по которому распределён заряд. Тогда при непрерывном распределении заряда в некотором объеме теорема Гаусса записывается в виде:

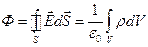. (6.6)

Если заряд распределен по объему или поверхности цилиндрического тела (равномерного в каждом сечении), используется линейная плотность заряда

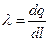, (6.7)

здесь 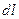- длина бесконечно малого отрезка цилиндра, - заряд, сосредоточенный на этом отрезке. В этом случае теорема Гаусса принимает вид:

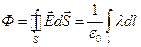. (6.8)

Теорема Гаусса связывает между собой величину заряда и напряжённость поля, которое им создаётся. Этим и определяется значение данной теоремы в электростатике. Она позволяет рассчитывать напряжённость, зная расположение зарядов в пространстве. В ряде случаев данный метод расчета полей значительно более простой, чем использование формулы напряженности поля точечного заряда и принципа суперпозиции.

Дата добавления: 2014-01-20