Поле бесконечной, равномерно заряженной плоскости

ПРИМЕНЕНИЯ ТЕОРЕМЫ ГАУССА К РАСЧЁТУ НЕКОТОРЫХ ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЕЙ.

В различных электрических устройствах, таких как конденсаторы, антенны, волноводы и т.п. приходится сталкиваться с заряженными поверхностями. Наиболее часто в таких устройствах заряды распределены по плоским, цилиндрическим и сферическим поверхностям. Расчёт электростатических полей, создаваемых такими заряженными поверхностями, проводится с использованием теоремы Гаусса.

Рассмотрим электростатическое поле бесконечной плоскости, заряженной с постоянной поверхностной плотностью 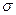. Для определенности будем считать заряд положительным. Рассмотрение бесконечной плоскости позволяет не учитывать краевых эффектов, имеющих место при конечных размерах плоскости. Поскольку плоскость бесконечная и 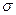постоянная, то в силу симметрии вектор 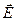напряжённости поля перпендикулярен к плоскости, и в точках, симметричных относительно плоскости, одинаков по модулю. Чтобы применить теорему Гаусса, надо мысленно выбрать произвольную замкнутую поверхность. В данном случае удобнее всего взять её в виде прямого цилиндра с осью, перпендикулярной к плоскости, и с основаниями площадью 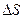, расположенными на одинаковом расстоянии от плоскости (рис. 7.1). Как видно из этого рисунка, линии напряжённости не пересекают боковую поверхность цилиндра. Поэтому поток напряжённости через неё равен нулю, и поток вектора 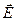сквозь замкнутую поверхность будет равен потоку через два основания, т.е. . Внутри поверхности заключен заряд 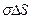. Согласно теореме Гаусса должно выполняться условие

,

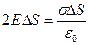из которого следует

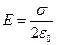. (7.1)

Рис. 7.1

Полученный нами результат не зависит от длины цилиндра. Это означает, что на любых расстояниях от плоскости напряженность поля одинакова по величине. Вид линий напряженности показан на рис. 7.2. Для отрицательно заряженной плоскости результат будет таким же, лишь направление вектора напряженности и линий напряженности изменится на противоположное.

Рис. 7.2

Если взять плоскость конечных размеров, то полученный выше результат будет справедлив только для точек, расстояние которых от края пластинки значительно превышает расстояние от самой пластинки. На рис. 7.3 область этих точек обведена пунктирной кривой. По мере удаления от плоскости или приближения к её краям поле будет все больше отличаться от поля бесконечной заряженной плоскости. На расстояниях, значительно превышающих размеры пластинки, создаваемое ею поле можно рассматривать как поле точечного заряда.

Рис. 7.3

Дата добавления: 2014-01-20