
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Сегнетоэлектрики. 3 страница
|
|
|
|
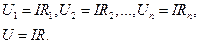 (23.3)
(23.3)
Подставим формулы (23.3) в выражение (23.2)
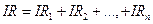 . (23.3)
. (23.3)
Поделим на силу тока 
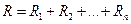 . (23.4)
. (23.4)
Выражение (23.4) позволяет рассчитывать сопротивление последовательного соединения проводников.
Рассмотрим параллельное соединение проводников (рис. 23.2). Параллельным соединением называется такое, при котором к одним и тем же двум узлам электрической цепи присоединены несколько ветвей. В этом случае напряжение на участках цепи одинаково
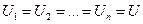 , (23.5)
, (23.5)
так как электрическое поле потенциально и работа по перенесению зарядов не зависит от формы пути. Потери зарядов на участках цепи нет, поэтому полный ток равен сумме токов на каждом из участков
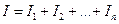 . (23.6)
. (23.6)
Согласно закону Ома токи в ветвях и общий ток определяются по формулам
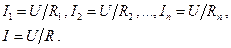 (23.7)
(23.7)
Подставим формулы (23.7) в выражение (23.6)
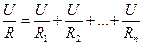 . (23.8)
. (23.8)
Поделим на напряжение 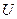
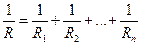 . (23.9)
. (23.9)
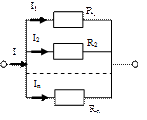 |
Выражение (23.9) позволяет рассчитывать сопротивление параллельного соединения проводников. При параллельном соединении величина обратная полному сопротивлению, равна сумме величин, обратных сопротивлений ветвей.
Рис. 23.2(Добавить напряжение)
При параллельном соединении полное сопротивление цепи всегда меньше самого малого из сопротивлений ветвей.
Если сопротивления всех 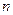 параллельно соединенных резисторов одинаковы и равны
параллельно соединенных резисторов одинаковы и равны 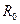 то общее сопротивление равно
то общее сопротивление равно
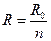 . (23.10)
. (23.10)
Сопротивление цепи, состоящей из 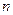 одинаковых параллельно соединенных резисторов, в
одинаковых параллельно соединенных резисторов, в 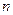 раз меньше сопротивления каждого из них.
раз меньше сопротивления каждого из них.
При параллельном соединении резисторов справедливо соотношение
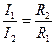 , (23.11)
, (23.11)
т.е. силы токов в ветвях параллельно соединенной цепи обратно пропорциональны сопротивлениям ветвей.
§24. Температурная зависимость сопротивления проводников и полупроводников.
В этом параграфе рассмотрим зависимость сопротивления проводников (имеются ввиду металлы) и полупроводников от температуры с точки зрения классической теории проводимости.
Начнем рассмотрение с проводников. Выясним сначала основные причины сопротивления в металлах. Все вещества, в том числе и металлы, могут существовать в трех агрегатных состояниях (твердом, жидком и газообразном). При переходе из газообразного (атомарного) состояния в жидкое начинает формироваться кристаллическая решетка. Атомы приходят во взаимодействие друг с другом. В результате чего крайние валентные электроны, которые слабо связаны с атомом, отрываются от ядра и становятся свободными (рис.24.1). Таким образом, свободных электронов (носителей заряда) в твердом металле очень много.
(Кристаллическая решетка со вободными электронами движущимися хаотично) Рис. 24.1.
В отсутствии электрического поля они движутся хаотично, подобно молекулам газа. Если поместить проводник в электрическое поле, то под его действием свободные электроны начинают направленное движение (рис. 24.2), т.е. возникает электрический ток. На своем пути электроны встречают узлы кристаллической решетки и сталкиваются с ними. Это первая причина сопротивления – столкновения с узлами кристаллической решетки.
(Кристаллическая решетка с направленно движущимися электронами) Рис. 24.1.
Как раннее было сказано, свободных электронов много и они хаотично движутся, хотя и существует преимущественное направление (направление электрического тока). Поэтому они сталкиваются между собой - это вторая причина сопротивления.
При увеличении температуры хаотичное движение свободных электронов усиливается и, следовательно, увеличивается число столкновений с узлами кристаллической решетки и между собой. Таким образом, увеличение температура приводит к увеличению сопротивления металлов. Изменение сопротивления, а значит и удельного сопротивления с температурой описывается линейным законом:
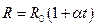 , (24.1)
, (24.1)
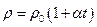 , (24.2)
, (24.2)
где 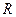 и
и 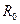 ,
, 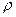 и
и 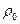 — соответственно сопротивления и удельные сопротивления проводника при температуре
— соответственно сопротивления и удельные сопротивления проводника при температуре 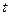 и
и 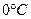 ;
; 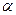 — температурный коэффициент сопротивления, для чистых металлов (при не очень низких температурах) близкий к
— температурный коэффициент сопротивления, для чистых металлов (при не очень низких температурах) близкий к 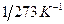 . Следовательно, температурная зависимость сопротивления может быть представлена в виде
. Следовательно, температурная зависимость сопротивления может быть представлена в виде
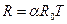 , (24.3)
, (24.3)
где 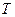 — термодинамическая температура.
— термодинамическая температура.
Зависимость сопротивления от температуры представлена на рис. 24.3 (кривая 1). При низких температурах наблюдается отступление от этой зависимости.
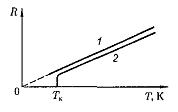 рис. 24.3
рис. 24.3
Впоследствии было обнаружено, что сопротивление многих металлов (например, Al, Pb, Zn и др.) и их сплавов при очень низких температурах 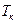 (0,14 — 20 К), называемых критическими, характерных для каждого вещества, скачкообразно уменьшается до нуля (кривая 2), т.е. металл становится абсолютным проводником. Впервые это явление, названное сверхпроводимостью, обнаружено в 1911г. Г. Камерлинг-Оннесом для ртути.
(0,14 — 20 К), называемых критическими, характерных для каждого вещества, скачкообразно уменьшается до нуля (кривая 2), т.е. металл становится абсолютным проводником. Впервые это явление, названное сверхпроводимостью, обнаружено в 1911г. Г. Камерлинг-Оннесом для ртути.
Явление сверхпроводимости объясняется на основе квантовой теории. Практическое использование сверхпроводящих материалов (в обмотках сверхпроводящих магнитов, в системах памяти ЭВМ и др.) затруднено из-за их низких критических температур. В настоящее время обнаружены и активно исследуются керамические материалы, обладающие сверхпроводимостью при температуре выше 140 К.
На зависимости электрического сопротивления металлов от температуры основано действие термометров сопротивления, которые позволяют по градуированной взаимосвязи сопротивления от температуры измерять температуру с точностью до 0,001 К. Термометры сопротивления, в которых в качестве рабочего вещества используются полупроводники, изготовленные по специальной технологии, называются термисторами. Они позволяют измерять температуру с точностью до миллионных долей кельвин.
Но температурная зависимость сопротивления полупроводников коренным образом отличается от зависимости металлов. Рассмотрим причины сопротивления в полупроводниках. У атомов полупроводников нет слабо связанных электронов на крайних энергетических уровнях. При формировании кристаллической решетки нет массового образования свободных электронов. Но некоторые электроны обладают энергией достаточной для отрыва от кристаллической решетки. При этом образуется пара носителей заряда – свободный электрон и дырка (рис.24.4). Дырка – квазичастица, обладающая положительным зарядом, по своей сути это вакантное место для электрона, в котором есть недостаток отрицательного заряда. Но носителей тока в полупроводниках, свободных электронов и дырок, мало – это основная причина сопротивления.
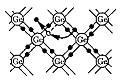 Рис. 24.4
Рис. 24.4
При повышении температуры все большее число электронов способны покинуть свои места. Увеличение числа носителей заряда ведет к уменьшению сопротивления. Зависимость сопротивления полупроводников от температуры имеет следующий вид
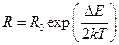 , (24.3)
, (24.3)
где 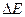 - энергия активации, минимальная энергия необходимая для отрыва электрона от кристаллической решетки (величина, постоянная для данного вещества),
- энергия активации, минимальная энергия необходимая для отрыва электрона от кристаллической решетки (величина, постоянная для данного вещества), 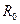 - условное сопротивление полупроводника при
- условное сопротивление полупроводника при 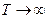 , константа, зависящая от физико-химических свойств полупроводника, а также от его геометрических размеров,
, константа, зависящая от физико-химических свойств полупроводника, а также от его геометрических размеров, 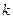 - постоянная Больцмана (
- постоянная Больцмана (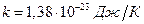 ),
), 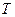 - термодинамическая температура. Сопротивление, а значит и удельное сопротивление, полупроводников убывает по экспоненциальному закону (рис.24.5).
- термодинамическая температура. Сопротивление, а значит и удельное сопротивление, полупроводников убывает по экспоненциальному закону (рис.24.5).
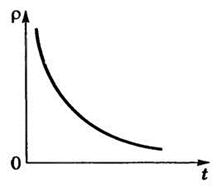 рис.24.5(заменить удельное сопротивление на сопротивление, температуру на термодинамическую температуру)
рис.24.5(заменить удельное сопротивление на сопротивление, температуру на термодинамическую температуру)
§25. Работа и мощность тока. Закон Джоуля – Ленца. КПД.
Рассмотрим однородный проводник, к концам которого приложено напряжение 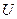 . За время
. За время 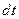 через сечение проводника переносится заряд
через сечение проводника переносится заряд 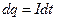 . При этом силы электростатического поля и сторонние силы совершают работу
. При этом силы электростатического поля и сторонние силы совершают работу
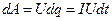 . (25.1)
. (25.1)
Если сопротивление проводника 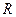 , то, используя закон Ома (22.1)
, то, используя закон Ома (22.1) 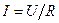 , получим, что работа тока
, получим, что работа тока
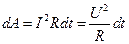 . (25.2)
. (25.2)
Из (25.1) и (25.2) следует, что мощность тока
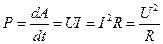 . (25.3)
. (25.3)
Работа тока выражается в джоулях (Дж), а мощность в ваттах (Вт).
Мощность, развиваемая током на участке цепи, может расходоваться на перемещение участка цепи или на протекание в нем химических реакций, или может превратиться в тепло. В случае, когда проводник неподвижен и химических реакций в нем не происходит, работа тока затрачивается на увеличение внутренней энергии проводника, в результате чего проводник нагревается. Принято говорить, что в проводнике выделяется тепло. По закону сохранения энергии
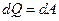 . (25.4)
. (25.4)
Таким образом, используя выражения (25.4), (25.1) и (25.2), получим
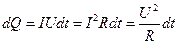 . (25.5)
. (25.5)
Выражение (25.5) представляет собой закон Джоуля —Ленца, экспериментально установленный независимо друг от друга Дж. Джоулем и Э. X. Ленцем.
Выделим в проводнике элементарный цилиндрический объем ось которого совпадает с направлением тока
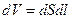 , (25.6)
, (25.6)
сопротивление которого
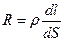 . (25.7)
. (25.7)
По закону Джоуля — Ленца за время dt в этом объеме выделится теплота
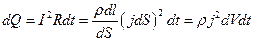 . (25.8)
. (25.8)
Введем новую величину – удельная тепловая мощность тока – это количество теплоты, выделяющееся за единицу времени в единице объема
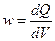 . (25.9)
. (25.9)
Измеряется эта величина в 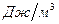 .
.
Удельная тепловая мощность тока равна
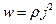 . (25.10)
. (25.10)
Используя дифференциальную форму закона Ома (22.8) 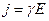 и соотношение (22.4)
и соотношение (22.4) 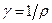 , получим
, получим
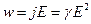 . (25.11)
. (25.11)
Формулы (25.10) и (25.11) являются обобщенным выражением закона Джоуля — Ленца в дифференциальной форме, пригодным для любого проводника.
Тепловое действие тока находит широкое применение в технике, которое началось с открытия в 1873 г. русским инженером А.Н.Лодыгиным (1847 — 1923) лампы накаливания. На нагревании проводников электрическим током основано действие электрических муфельных печей, электрической дуги (открыта русским инженером В. В. Петровым (1761 —1834)), контактной электросварки, бытовых электронагревательных приборов и т. д.
Источником тока выделяется мощность, называемая полной мощностью и определяемая формулой
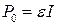 , (25.12)
, (25.12)
где 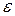 - ЭДС источника тока,
- ЭДС источника тока, 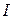 - сила тока в цепи. Формула (25.3) учитывает только часть полной мощности, которая выделяется на нагрузке и называется полезной мощностью. Остальная часть расходуется в источнике тока и подводящих проводах и оказывается бесполезной.
- сила тока в цепи. Формула (25.3) учитывает только часть полной мощности, которая выделяется на нагрузке и называется полезной мощностью. Остальная часть расходуется в источнике тока и подводящих проводах и оказывается бесполезной.
Отношение полезной мощности ко всей мощности, развиваемой ЭДС в цепи, определяет коэффициент полезного действия источника тока:
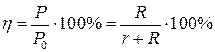 , (25.13)
, (25.13)
где  - сопротивление внешней цепи,
- сопротивление внешней цепи,  - сопротивление источника тока.
- сопротивление источника тока.
КПД измеряется в процентах.
Из формулы (25.13) следует, что КПД будет тем больше, чем больше сопротивление нагрузки по сравнению с сопротивлением источника тока. Поэтому сопротивление источника стремяться делать как можно меньшим.
Мощность, развиваемая источником тока, зависит от сопротивления нагрузки. С ростом  полная мощность убывает, стемясь к нулю при
полная мощность убывает, стемясь к нулю при 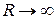 .
.
Полезная мощность имеет максимум при  =
= , т.е. чтобы отобрать от данной ЭДС наибольшую полезную мощность, нужно взять сопротивление нагрузки, равное сопротивлению источника тока. КПД в этом случае составит
, т.е. чтобы отобрать от данной ЭДС наибольшую полезную мощность, нужно взять сопротивление нагрузки, равное сопротивлению источника тока. КПД в этом случае составит 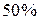 .
.
§26. Правила Кирхгофа.
При разработке электрических и радиотехнических схем приходится сталкиваться с очень сложными разветвлёнными электрическими цепями. Непосредственный расчет разветвленных цепей, содержащих несколько замкнутых контуров (рис. 26.1) (контуры могут иметь общие участки, каждый из контуров может иметь несколько источников тока и т.д.), довольно сложен. Эта задача более просто решается с помощью двух правил Кирхгофа.
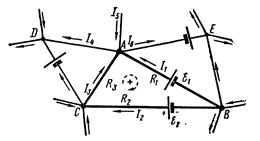 рис. 26.1
рис. 26.1
Любая точка разветвления цепи, в которой сходится не менее трех проводников с током, называется узлом. На рис. 26.1 А, B, C, D, E – узлы. Ток, входящий в узел, считается положительным, а ток, выходящий из узла — отрицательным.
Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в
узле, равна нулю:
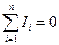 , (26.1)
, (26.1)
где 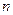 - число токов сходящихся в узле.
- число токов сходящихся в узле.
Первое правило Кирхгофа вытекает из закона сохранения электрического заряда. Действительно, в случае установившегося постоянного тока ни в одной точке проводника и ни на одном его участке не должны накапливаться электрические заряды. В противном случае токи не могли бы оставаться постоянными.
Второе правило Кирхгофа вытекает из того, что электрическое напряжение по замкнутому контуру равно нулю, а значит, это правило есть следствие основного свойства электростатического поля, согласно которому работа при движении заряда по замкнутому контуру равна нулю. Оно является обобщением закона Ома для разветвленных цепей и применяется для замкнутых контуров. На рис. 26.1 контур САВ – замкнутый.
Второе правило Кирхгофа: алгебраическая сумма произведений сил токов на сопротивления (напряжений) в ветвях любого замкнутого контура равна алгебраической сумме ЭДС, встречающихся в этом контуре:
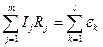 , (26.2)
, (26.2)
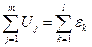 , (26.3)
, (26.3)
где 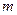 и
и 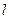 - число сопротивлений и источников тока в контуре соответственно.
- число сопротивлений и источников тока в контуре соответственно.
Необходимо отметить, что сопротивления 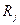 включают в себя и внутренние сопротивления источников тока.
включают в себя и внутренние сопротивления источников тока.
При применении этого правила выбирается какое-нибудь направление обхода (по или против часовой стрелки) и уславливаются о правиле знаков:
а) если ток в данной ветви течет в направлении обхода контура, то соответствующие произведения 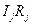 берутся со знаком плюс, в противном случае — со знаком минус;
берутся со знаком плюс, в противном случае — со знаком минус;
б) если в направлении обхода внутри источника происходит переход от отрицательного полюса к положительному, то ЭДС берётся со знаком плюс, в противном случае - с минусом.
При решении задач рекомендуется следующий порядок расчета сложной цепи постоянного тока:
1. Выбрать произвольное направление токов на всех участках цепи; действительное направление токов определится при решении задачи: если искомый ток получится положительным, то его направление было выбрано правильно, отрицательным — его истинное направление противоположно выбранному.
2. Подсчитать число узлов в цепи 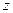 . Записать выражения (26.1) для каждого из
. Записать выражения (26.1) для каждого из 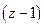 узлов. Уравнение (26.1) для
узлов. Уравнение (26.1) для 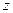 -гo узла ничего нового не дает, так как оно является простым следствием предыдущих
-гo узла ничего нового не дает, так как оно является простым следствием предыдущих 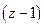 уравнений.
уравнений.
3. Выделить произвольные замкнутые контуры в цепи и, условившись о направлении обхода, записать для них систему уравнений (26.2). Уравнения (26.2) следует писать не для всех контуров, так как часть из этих уравнений является следствием предыдущих. Каждый рассматриваемый контур должен содержать хотя бы один элемент, не содержащийся в предыдущих контурах. Оказывается, что в разветвленной цепи, состоящей из 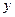 ветвей (участков цепи между соседними узлами) и
ветвей (участков цепи между соседними узлами) и 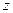 узлов, число возможных независимых уравнений (26.2) равно
узлов, число возможных независимых уравнений (26.2) равно 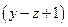 .
.
Должно быть составлено столько уравнений, чтобы их число было равно числу искомых величин, так же в систему уравнений должны входить все сопротивления и ЭДС рассматриваемой цепи.
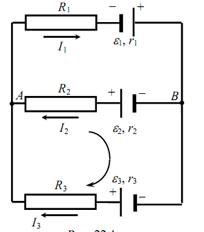 Рис. 26.2
Рис. 26.2
Составим систему уравнений, применяя правила Кирхгофа, для цепи изображенной на рис. 26.2. Направление токов 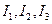 выбрали произвольно, как обозначено на рисунке. По первому правилу составим 1 уравнение (на одно меньше количества узлов) для узла А. По второму правилу составим 2 уравнения для контуров А
выбрали произвольно, как обозначено на рисунке. По первому правилу составим 1 уравнение (на одно меньше количества узлов) для узла А. По второму правилу составим 2 уравнения для контуров А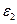 В
В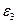 А и А
А и А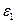 В
В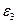 А. Направление обхода контуров выбрали по часовой стрелке.
А. Направление обхода контуров выбрали по часовой стрелке.
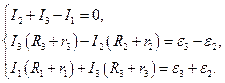 (26.4)
(26.4)
Зная величины сопротивлений и ЭДС, можно определить силы токов, решив эту систему уравнений.
§27. Классическая теория электропроводности.
Носителями тока в металлах являются свободные электроны, т.е. электроны, слабо связанные с ионами кристаллической решетки металла. Это представление о природе носителей тока в металлах основывается на электронной теории проводимости металлов, созданной немецким физиком П. Друде (1863 — 1906) и разработанной впоследствии нидерландским физиком X. Лоренцем, а также на ряде классических опытов, подтверждающих положения электронной теории.
Первый из таких опытов — опыт Рикке (1901), в котором в течение года электрический ток пропускался через три последовательно соединенных с тщательно отшлифованными торцами металлических цилиндра (Сu, А1, Сu) одинакового радиуса. Несмотря на то что общий заряд, прошедший через эти цилиндры, достигал огромного значения (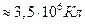 ), никаких, даже микроскопических, следов переноса вещества не обнаружилось. Это явилось
), никаких, даже микроскопических, следов переноса вещества не обнаружилось. Это явилось
экспериментальным доказательством того, что ионы в металлах не участвуют в переносе электричества, а перенос заряда в металлах осуществляется частицами, которые являются общими для всех металлов. Такими частицами могли быть открытые в 1897 г. английским физиком Д.Томсоном (1856 — 1940) электроны.
Для доказательства этого предположения необходимо было определить знак и величину удельного заряда носителей (отношение заряда носителя к его массе). Идея подобных опытов заключалась в следующем: если в металле имеются подвижные, слабо связанные с решеткой носители тока, то при резком торможении проводника эти частицы должны по инерции смещаться вперед, как смещаются вперед пассажиры, стоящие в вагоне при его торможении. Результатом смещения зарядов должен быть импульс тока; по направлению тока можно определить знак носителей тока, а зная размеры и сопротивление проводника, можно вычислить удельный заряд носителей.
Идея этих опытов (1913) и их качественное воплощение принадлежат российским физикам С.Л.Мандельштаму (1879-1944) и Н.Д.Папалекси (1880-1947). Эти опыты в 1916 г. были усовершенствованы и проведены американским физиком Р.Толменом (1881 — 1948) и ранее шотландским физиком Б.Стюартом (1828—1887). Ими экспериментально доказано, что носители тока в металлах имеют отрицательный заряд, а их удельный заряд приблизительно одинаков для всех исследованных металлов. По значению удельного заряда носителей электрического тока и по определенному ранее Р. Милликеном элементарному электрическому заряду была определена их масса. Оказалось, что значения удельного заряда и массы носителей тока и электронов, движущихся в вакууме, совпадали. Таким образом, было окончательно доказано, что носителями электрического тока в металлах являются свободные электроны.
Существование свободных электронов в металлах можно объяснить следующим образом (было рассмотрено ранее в §24): при образовании кристаллической решетки металла (в результате сближения изолированных атомов) валентные электроны, сравнительно слабо связанные с атомными ядрами, отрываются от атомов металла, становятся «свободными» и могут перемещаться по всему объему. Таким образом, в узлах кристаллической решетки располагаются ионы металла, а между ними хаотически движутся свободные электроны, образуя своеобразный электронный газ, обладающий, согласно электронной теории металлов, свойствами идеального газа.
Электроны проводимости при своем движении сталкиваются с ионами решетки, в результате чего устанавливается термодинамическое равновесие между электронным газом и решеткой. По теории Друде-Лоренца, электроны обладают такой же энергией теплового движения, как и молекулы одноатомного газа. Поэтому, применяя выводы молекулярно-кинетической теории, можно найти среднюю скорость теплового движения электронов
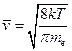 , (27.1)
, (27.1)
где 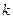 - постоянная Больцмана,
- постоянная Больцмана, 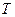 - термодинамическая температура,
- термодинамическая температура, 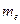 - масса электрона. Используя выражение (27.1) скорость теплового движения свободных электронов, при
- масса электрона. Используя выражение (27.1) скорость теплового движения свободных электронов, при 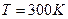 , равна
, равна 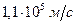 . Тепловое движение электронов, являясь хаотическим, не может привести к возникновению тока.
. Тепловое движение электронов, являясь хаотическим, не может привести к возникновению тока.
При наложении внешнего электрического поля на металлический проводник кроме теплового движения электронов происходит их упорядоченное движение, т. е. возникает электрический ток. Среднюю скорость 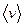 упорядоченного движения электронов можно оценить согласно формуле (20.6) для плотности тока:
упорядоченного движения электронов можно оценить согласно формуле (20.6) для плотности тока: 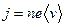 . Выбрав допустимую плотность тока, например для медных проводов 107 А/м2, получим, что при концентрации носителей тока
. Выбрав допустимую плотность тока, например для медных проводов 107 А/м2, получим, что при концентрации носителей тока 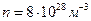 средняя скорость
средняя скорость 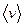 упорядоченного движения электронов равна
упорядоченного движения электронов равна 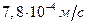 . Следовательно,
. Следовательно, 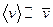 , т.е. даже при очень больших плотностях тока средняя скорость упорядоченного движения электронов, обусловливающего электрический ток, значительно меньше их скорости теплового движения. Поэтому при вычислениях результирующую скорость
, т.е. даже при очень больших плотностях тока средняя скорость упорядоченного движения электронов, обусловливающего электрический ток, значительно меньше их скорости теплового движения. Поэтому при вычислениях результирующую скорость 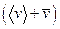 можно заменять скоростью теплового движения
можно заменять скоростью теплового движения 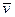 .
.
Казалось бы, полученный результат противоречит факту практически мгновенной передачи электрических сигналов на большие расстояния. Дело в том, что замыкание электрической цепи влечет за собой распространение электрического поля со скоростью с (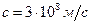 ). Через время
). Через время 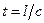 (
(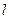 — длина цепи) вдоль цепи установится стационарное электрическое поле и в ней начнется упорядоченное движение электронов. Поэтому электрический ток возникает в цепи практически одновременно с ее замыканием.
— длина цепи) вдоль цепи установится стационарное электрическое поле и в ней начнется упорядоченное движение электронов. Поэтому электрический ток возникает в цепи практически одновременно с ее замыканием.
С помощью классической электронной теории металлов удалось теоретически получить закон Ома для однородного участка цепи, закон Джоуля-Ленца. Однако эта теория не в состоянии объяснить целый ряд явлений, наблюдающихся на опыте.
В классической электронной теории сопротивление пропорционально квадратному корню из абсолютной температуры 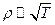 . Экспериментально же установлено, что в достаточно широком интервале температур
. Экспериментально же установлено, что в достаточно широком интервале температур 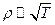 (см. §24).
(см. §24).
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 425; Нарушение авторских прав?; Мы поможем в написании вашей работы!