
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вычисление двойного интеграла
|
|
|
|
Рассмотрение вопроса о вычислении двойного интеграла будем связывать, в первую очередь, с формой области D, последовательно рассмотрев случая, каждый следующий, из которых обобщает предыдущий.
I случай. Область D – прямоугольник (рисунок 4).
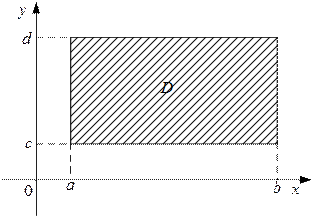
Рисунок 4
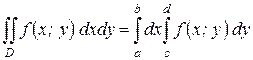
| (1.1) |

| (1.2) |
Для того, чтобы найти двойной интеграл по прямоугольной области D необходимо проинтегрировать функцию 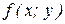 по одной из переменных в пределах ее фактического изменения, считая другую переменную фиксированной величиной (константой), а затем вычислить интеграл от функции другой переменной в пределах ее фактического изменения.
по одной из переменных в пределах ее фактического изменения, считая другую переменную фиксированной величиной (константой), а затем вычислить интеграл от функции другой переменной в пределах ее фактического изменения.
II случай. Область D – простая область, т.е. такая область, что любая прямая параллельная одной из координатных осей пересекает границу области не более чем в двух точках. Исключения могут составлять участки границы параллельные координатным осям (рисунок 5).
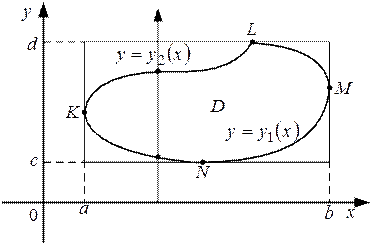
Рисунок 5
Поместим эту область внутрь прямоугольника стороны, которого параллельны осям и касаются границы области D.
Пусть дуга 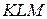 задается уравнением:
задается уравнением: 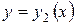 , а дуга
, а дуга 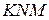 уравнением:
уравнением: 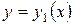 . Рассуждая аналогично случаю I, приходим к формуле:
. Рассуждая аналогично случаю I, приходим к формуле:
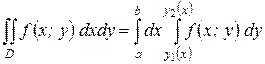
| (1.3) |
Получим другую формулу, предварительно предположив, что дуга 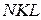 задается уравнением:
задается уравнением: 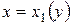 , а дуга
, а дуга 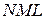 уравнением:
уравнением: 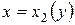 . Приходим к формуле:
. Приходим к формуле:
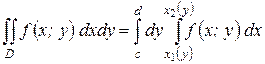
| (1.4) |
Для того, чтобы вычислить двойной интеграл по простой области D, необходимо проинтегрировать функцию 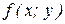 по одной из переменных в пределах ее фактического изменения, а затем полученную функцию другой переменной проинтегрировать по этой переменой в пределах ее максимального изменения.
по одной из переменных в пределах ее фактического изменения, а затем полученную функцию другой переменной проинтегрировать по этой переменой в пределах ее максимального изменения.
Процедура применения формул (1.3) и (1.4) называется кратным (или повторным) интегрированием, а переход от правой части формулы (1.3) к правой части формулы (1.4) (или наоборот) называется изменением порядка интегрирования в двойном интеграле. При этом 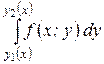 называют внутренним интегралом.
называют внутренним интегралом.
Замечание. 1) Формулы (1.3) и (1.4) справедливы и в случае когда 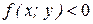 ,
, 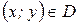 .
.
2) Если область D простая в обоих направлениях, то двойной интеграл можно вычислять как по формуле (1.3), так и формуле (1.4), при этом выбирается то направление интегрирования, которое приводит к меньшему числу вычислений.
3) Полезно помнить, что внешние пределы в двукратном интеграле постоянны, а внутренние переменные.
III случай. Область D – произвольная область (рисунок 6).

Рисунок 6
В этом случае область D при помощи прямых параллельных осям можно разбить на конечное число простых областей. По каждой из этих областей интеграл считается как в случае II, отсюда следует формула:
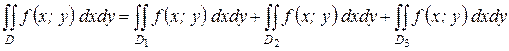 .
.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 652; Нарушение авторских прав?; Мы поможем в написании вашей работы!